【コラム】イェイツのカイ二乗検定について
カイ二乗検定とは
クロス集計の属性差を知るためにχ(カイ)二乗検定(または独立性の検定)を使うケースが多いと思います。
カイ二乗検定をざっくり説明するならば「このクロス表の数値はランダム(乱数)で作った表とどの程度ズレてるか」を知る方法で
そのズレがカイ二乗分布と著しくズレてるなら有意に差がある、と評価します。
\[
\chi^2 = \sum\frac{(観測値-期待値)^2}{期待値}
\]
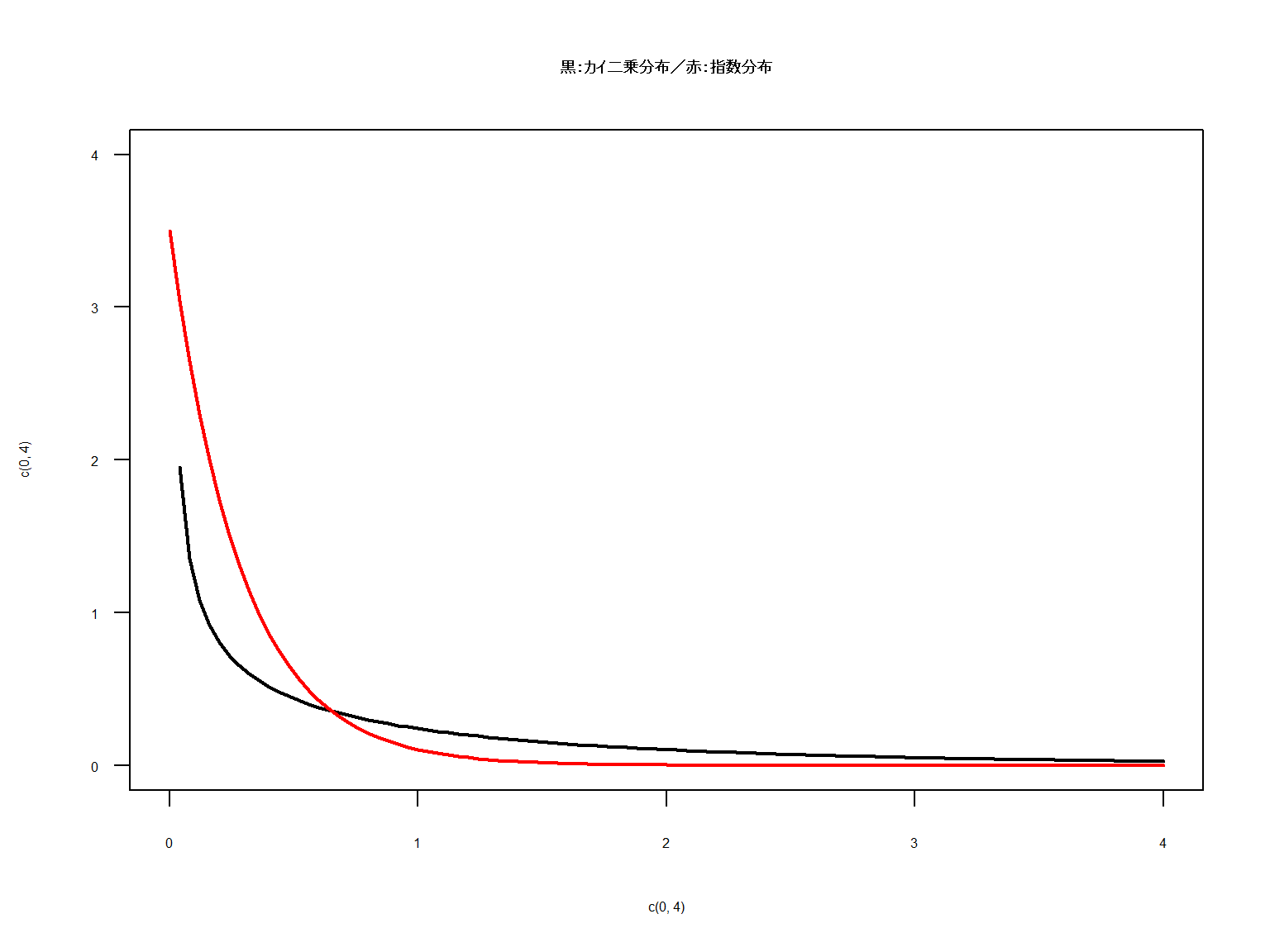
カイ二乗分布はt分布と同様に自由度というパラメータのみで生成されます。
自由度が小さいほど分布の形は指数分布のようにキュッとした形になります。
これは自由度が小さいときほどズレは小さいことを示しているのですが
収集されたデータのサンプル数は影響がないのでしょうか。
乱数シミュレーション
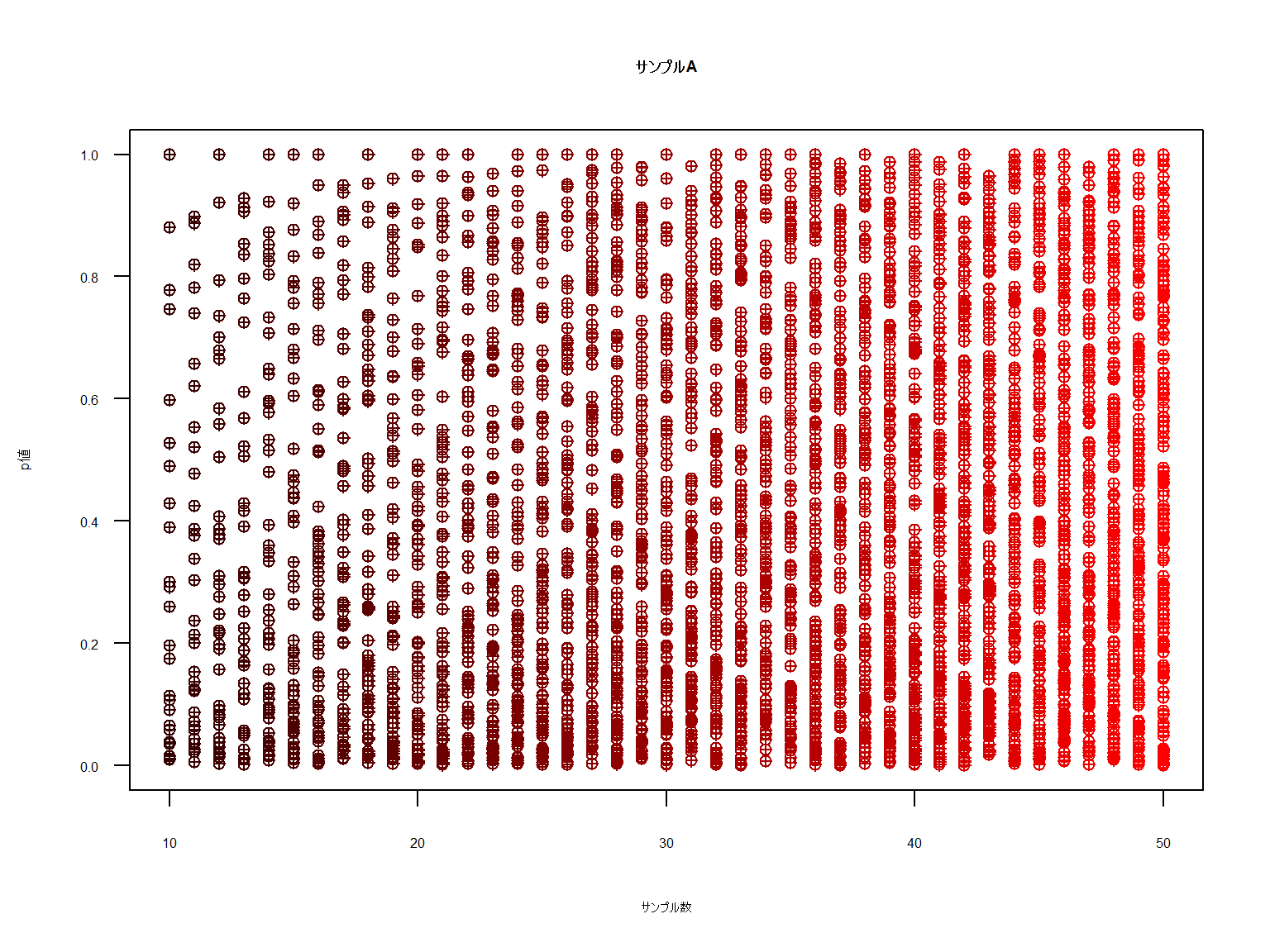
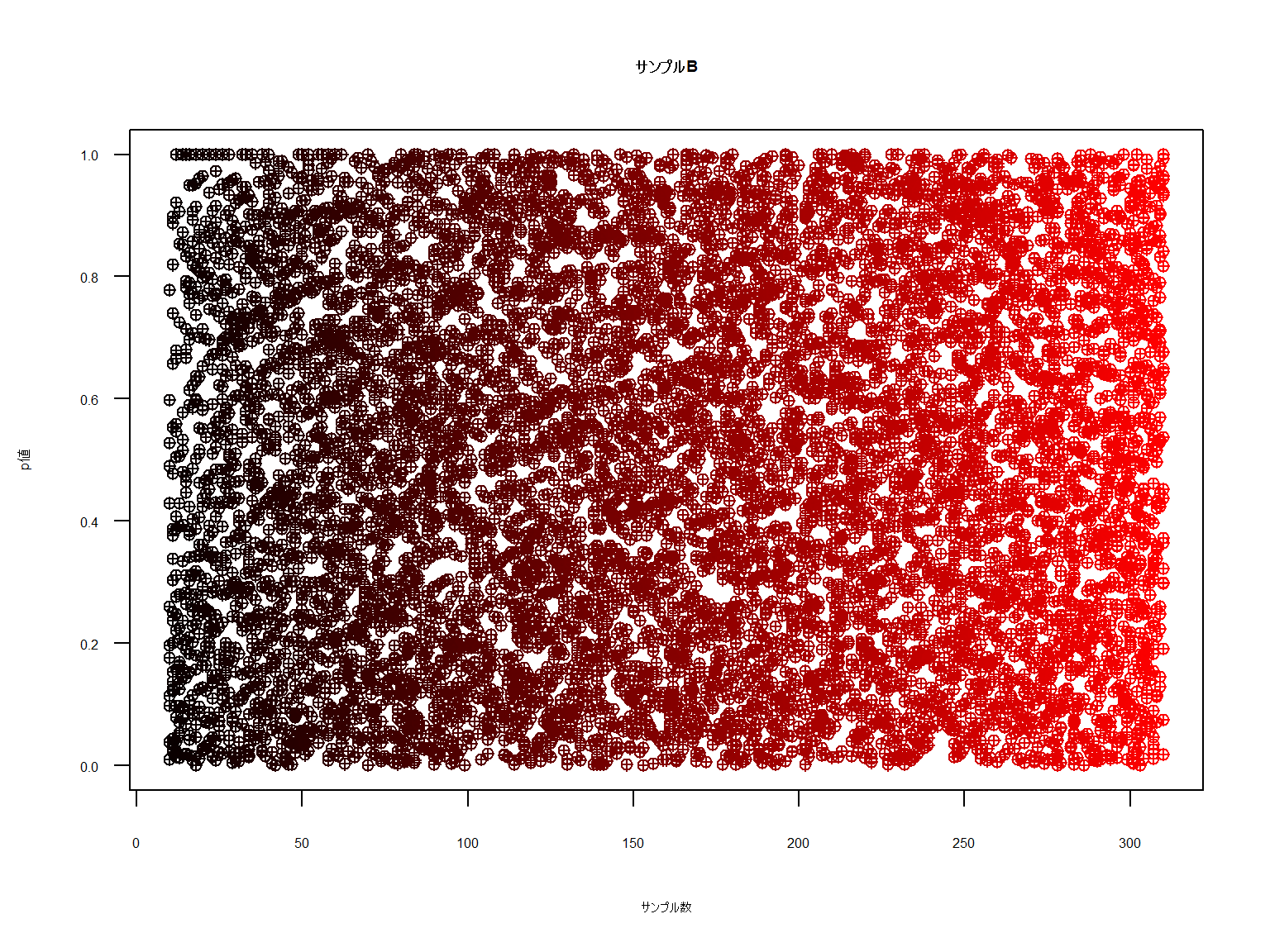
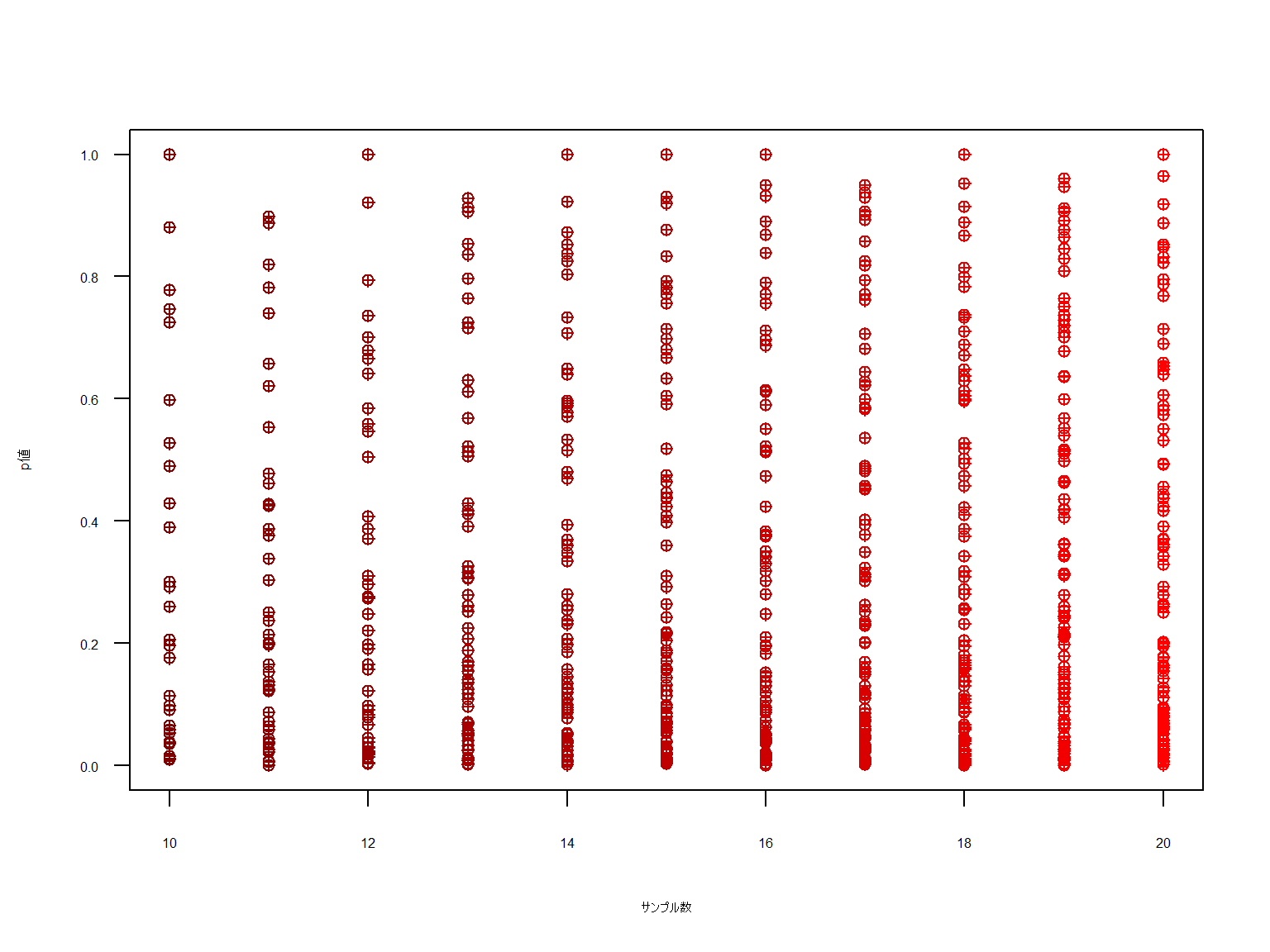
下図は一様分布による2元クロス表を1万回出現させた際のカイ二乗検定のp値です。
サンプルAは結果の総和が40程度まで、サンプルBは300程度までの出力です。
一様分布のため本来であれば「差」は出ず、p値の分布はバラバラになるはずです。
いかがでしょうか。サンプル数が極端に少ないケースの一部でp値が下に寄っているように見えますが
N数が増大していくと均等にp値が散布されていることがわかります。
ただちょっとわかりにくいのでヒストグラムも見てみましょう。
散布図同様に一様性が確認されました。
イェイツの補正とは何をするのか
カイ二乗分布本来の性質は、連続性のある数値を二乗和した数値の分布のため
クロス集計表のように離散的な数値では誤差が生じるのではないか、補正したほうが良いのではないか
という発案から生まれた手法です(間違ってたらすいません)。
\[
\chi^2_{Ya} = \sum \frac{(|観測値 – 期待値| – 0.5)^2}{期待値}\\
\]
こんな具合に誤差の絶対値から0.5引いた数字を二乗しています。
これは
\[
\chi^2 = \sum\frac{(観測値-期待値)^2}{期待値}
\]
本来のカイ二乗検定と比べてどのように補正されるのでしょうか。
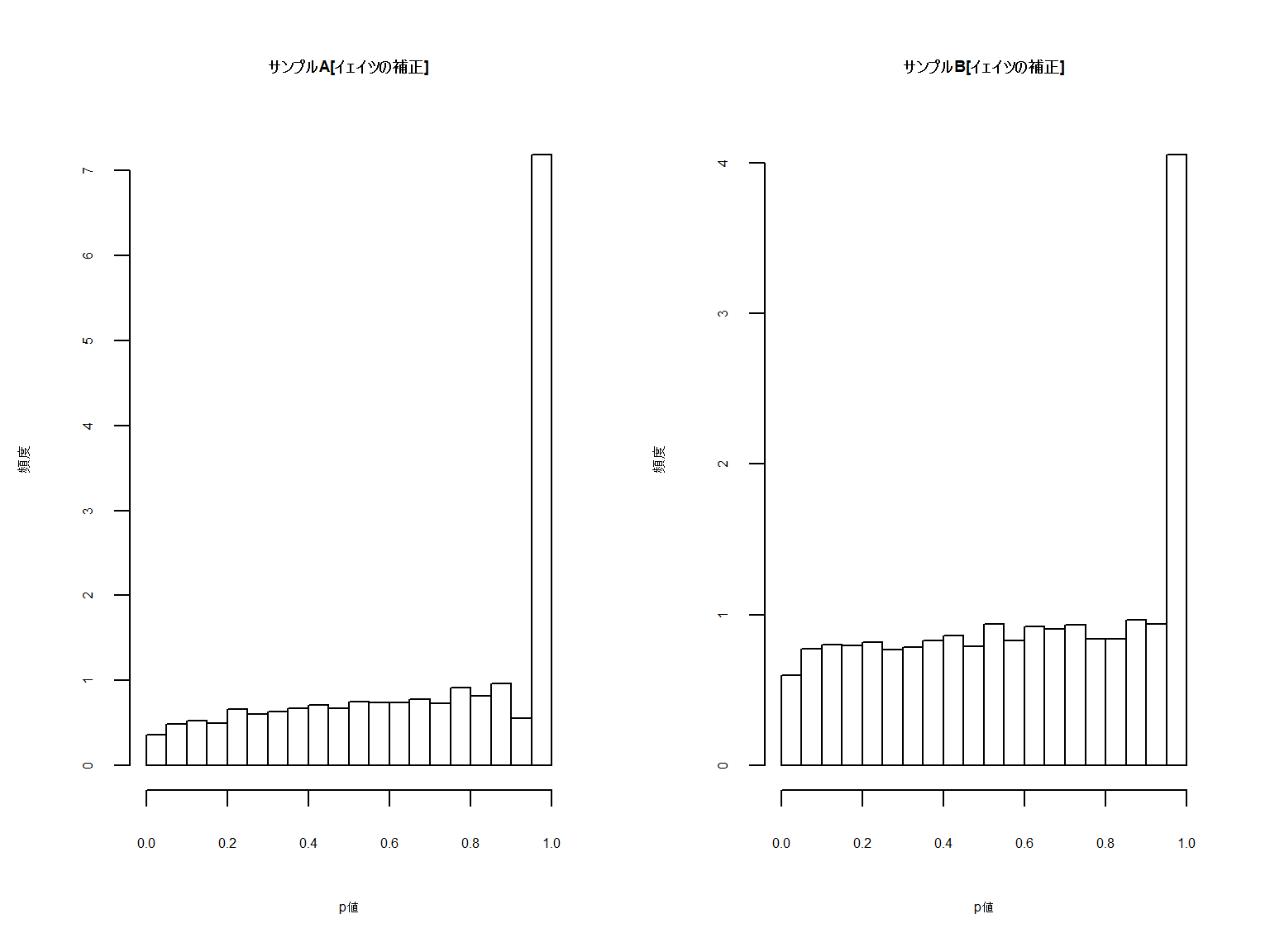
先程の結果と同じデータに補正を掛けて再計算しました。
おおよそ等しく分布していたp値が極端に1付近へ寄っていることがわかります。
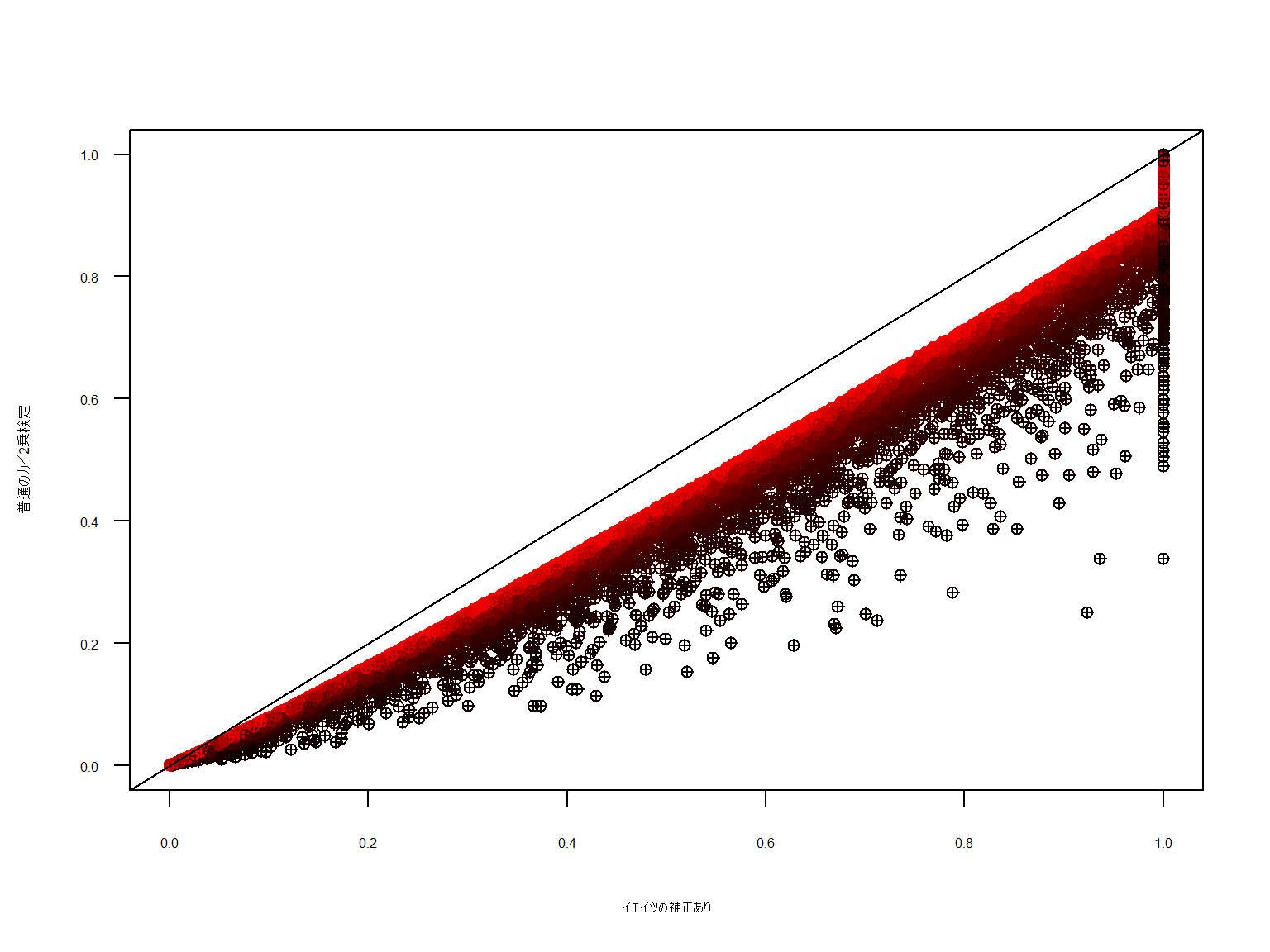
今度は通常のカイ二乗検定と補正した場合の比較散布図です。
※Rのカイ二乗検定関数[chisq.test]を使用しているため手計算の分布とは異なります(この件は後日整理して掲載予定)。
真ん中の直線はy=xの直線ですが、イエイツの補正が掛かっているほうがp値が高めに掛かっています(通常では有意となるものがならない)。
また赤い色はサンプル数が多いことを示していますが何らかの踏み越えられない空間的な隔たりを感じます。
数式を観察してみる。
下記の\(|観測値 – 期待値|\)を「絶対誤差」という名前に変えて比較してみましょう。
\[
絶対誤差 = |観測値 – 期待値|とする\\
(絶対誤差 – 0.5)^2 = 絶対誤差^2 – (絶対誤差 -0.25)\\
絶対誤差^2 = (|観測値 – 期待値|)^2 = (観測値 – 期待値)^2
\]
これは通常のカイ二乗検定の数式の上部と一致します。
\[
\chi^2 = \sum\frac{(観測値-期待値)^2}{期待値}
\]
つまり通常のカイ二乗検定よりも\(- (絶対誤差 -0.25)\)だけ二元表のそれぞれの計算でマイナス補正が掛かっていることがわかります。
※観測値=期待値の場合のみ+0.25ずつ補正されますが、そのあたりは別記事を作成予定です。
この補正が先の図の踏み越えられない空間を作っていたのですね。
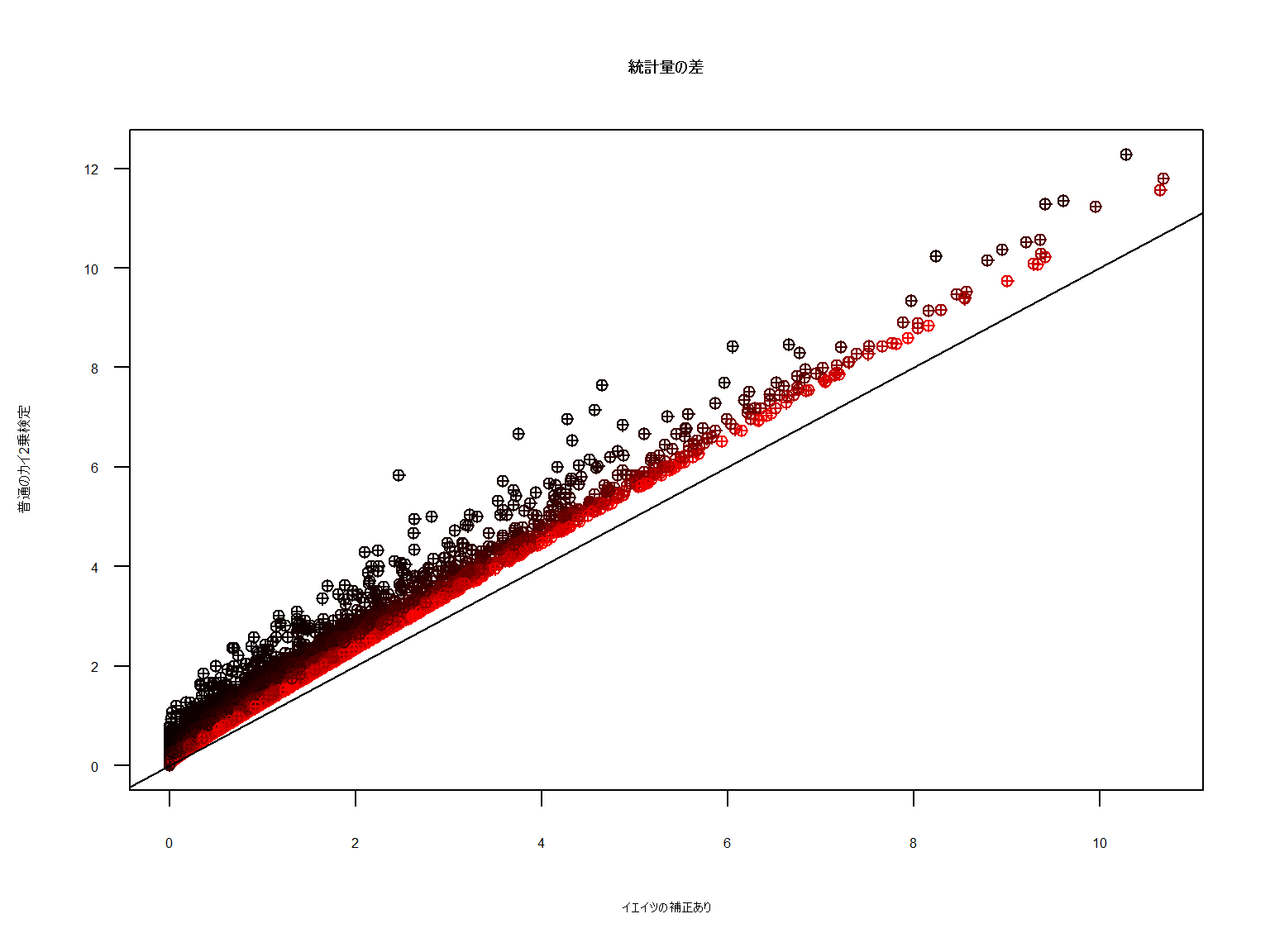
こちらはp値から統計量を復元し比較した図です。p値とは向きが異なるものの切り取られた空間分の補正が確認されました。
クルッと回すとパズルのようにはまりそうです。
着色はRGB(N数,イエイツのP値,普通のP値)です。キレイですねー。
補正は強く掛かり、また「掛かり過ぎる」という指摘がされるイエイツの補正ですが
N数が増加していくとその差が徐々になくなっていくことがわかります。
二元表で最低でも1つの集計で5以下の数値がある場合はこの補正が推奨されますが
観測値=期待値の場合でも統計量が加算されるため、分野によっては通常のカイ二乗検定を推奨するケースもあるみたいです。
(Rではサンプル数を問わずデフォルトで補正が掛かります)
カサ増ししたデータで同じことをやってみる
先の記事で有意差が出ないデータをなんとかする方法を紹介しました。
実際にはなんともならない、ただの数値遊びではありますが、試しに同じことを今回のロジックで計算します。
処理はサンプル数が少ない有意差の出なそうな二元表を作成し、それをランダムで倍加させました。
先のようにランダムなデータのため一様性が保てるはずですが。。。
元のデータを極端に歪めていることがわかります。
あらためてやってはいけない処理だということがわかりました。