相関係数について|Excel(エクセル)で学ぶデータ分析ブログ
■相関係数とは?
Wikipedia より(一部編集)
相関係数(correlation coefficient)とは、2 つの確率変数の間の相関を示す統計学的指標である。統計値や確率変数の散らばり具合(ばらつき)を表す数値のひとつ。
平均や分散、標準偏差などは1つのデータに対する指標として扱ってきましたが、
例えば「身長と体重」、「年齢と年収」、「理科と数学」など、世の中の傾向を読む際には通常2つ以上のデータを元に指標を作っていくことが主となってきます。
もちろん、結果的に使用するのは平均や分散などの指標にはなりますが、
それらをいくつかのデータ間(専門的には変数と呼びます)に掛け合わせることで数値を計算し、その数値を読み取ることでデータの評価をしていきます。
読み取る方法と計算過程、どちらを先に紹介すべきか悩みましたが、まずは計算の過程から紹介させていただきます。
■エクセルでの導きかた
例えば理科が得意な学生は数学も得意で「理数系」などと言われることが多々あります。
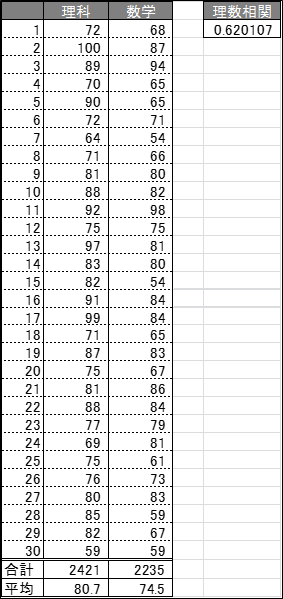
右上部に記載の値がこのクラス30名の理数テストに関する相関係数です。
0.62ということで、強めに出てますねー。
関数は【=CORREL(B2:B31,C2:C31)】というものを使用することで一発で出ます。
しかし、現在出力されている情報だけでは計算過程がまったくわかりません。
ということで、簡単な関数を用いて計算過程を紹介していきましょう。
(下部に出ている「合計、平均、分散」に関しては他記事にて詳細を書いてますので割愛します)
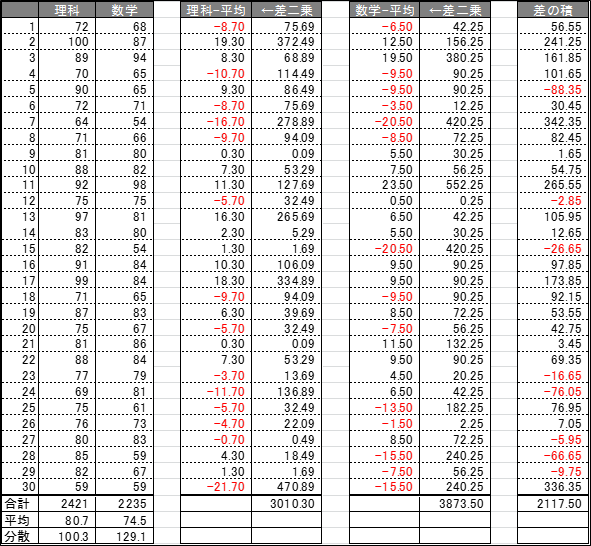
先ほどのデータの右側に赤くなったり黒くなったり桁数が増えたりして情報が増えております。
まず、「理科-平均」と書いてある指標から説明していきます。
「理科-平均」の列:
1行目であれば、理科の点数【72】から平均値【80.7】を引いた差【-8.70】が表示されています。同様に「得点-平均」を繰り返すことでデータの中心からの距離がわかります。
「差の二乗」の列:
すぐ隣の値を二乗しています。中心からの距離を取る際には正負の符号はあまり意味を持ちませんので、このように二乗することで(-)の符号を消します。また、合計の行にはそれらの値を全て足した数値が出ています。いわば中心からの距離(誤差)を積み重ねた数値でしょうか。
「数学-平均」と「差の二乗」の列も上記と同様です。
「差の積」の値は1行目を例にすれば「理科-平均」の【-8.70】と「数学-平均」の【-6.50】を掛け合わせた【56.55】が出力されています。
これもまた下部にて合計が計算されていますが、今度は(+)×(-)=(-)という値が少なからず出ることになるので差の二乗の合計値を越えない数値が出そうなことが直観的にわかります。
ここまで来たら、細かい理論的な部分はおいておいて、計算自体は可能です。
A:差の積の合計【2117.50】
B:理科の差の二乗の合計【3010.30】
C:数学の差の二乗の合計【3873.50】
上記3つを下記のように計算します。
=A/{(B×C)の平方根}
=2117.50/{(3010.30×3873.50)の平方根}
=2117.50/{(11,660,397.05)の平方根}
=2117.50/3,414.73
=0.620107…
いかがでしょうか? 先ほど紹介した
関数【=CORREL(B2:B31,C2:C31)】と同様の結果が出ております。
![]()
■相関係数の使い方
前述にて計算過程はなんとなくイメージしていただけたかと思います。
でも、肝心なのは「読み方」ですよね?
下記表は弊社ナレッジで分析をお預かりした際に、私が口頭で取るリアクション表です。
※相関係数の値は必ず-1~+1の間になります。

先ほどの値、0.62であれば「相関がありますね」というと思います。
何を言っているんだ、という感じだと思いますので、グラフ化してみました。
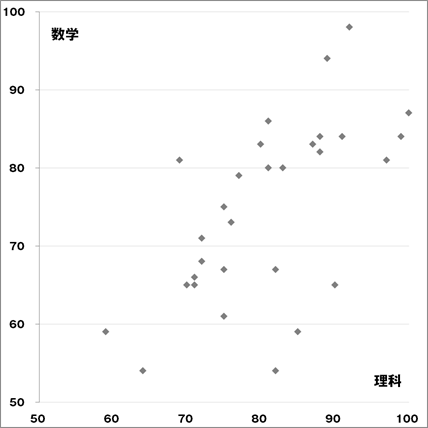
言葉で説明をするとすれば、
「数学の得点が高い(または低い)学生は、理科の得点も高い(または低い)傾向にあり、相関係数は0.62と高い正の相関関係にある」といった感じでしょうか。
データの散布がなんとなく右肩上がりになっているように見えませんか? 専門的には「正の相関」が出ていると表現します。
逆に左肩上がりになっているデータは「一方の値が高い(または低い)場合にもう一方のデータは低い(または高い)ため、負の相関関係にある」と表現します(値はマイナスの符号になります)。
また、データによって上がったり下がったりとバラバラの場合には相関係数が0に近づくため、「無相関」と表現します。
このように、データのバラつきが「直線に近づくほど数値は1に近づき、右肩上がり=プラス、左肩上がり=マイナスとなる。逆にデータがバラつくほど数値は0に近づく」指標を相関係数と呼びます。
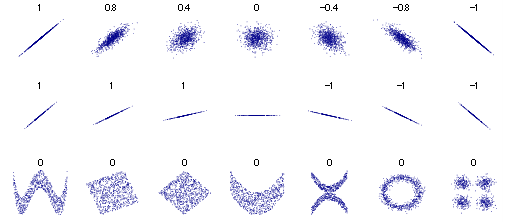
wikipediaより
■相関係数のまとめ
相関係数はデータ(変数)間の相関性を読み解くために便利な指標です。
但し、細かく定義する場合には下記の条件が前提となります。
・平均値がデータのバラつきにおいて中心に位置する
・標準偏差の±うちにほとんどの値が含まれている
専門的には「正規分布を仮定する」とか「パラメトリックなデータ」とか言いますが、この余白はそれを書くには狭すぎ(?) ますので、また深堀りした記事にて紹介させていただきます。
ちなみに、上述の説明で紹介した相関係数は正式には「ピアソンの積率相関係数」と呼ばれています。積率とかピアソンとかよくわかりませんね。ナンダソレハっていう感じです。
他にも
・スピアマンの順位相関係数
・ケンドールの順位相関係数
なんていうものもありますが、ますます意味がわかりませんので紹介はまた別の機会に。
→他記事 無相関について。