【コラム】エクセルの関数(分散、標準偏差、共分散、相関係数)について|Excel(エクセル)で学ぶデータ分析ブログ
※ざっくり読み解く 多変量解析始めました。
■母集団と母集団の推定によるエクセル関数の使い分け
エクセルには「分散」「標準偏差」「共分散」に対して下記のように細かい使い分けがあります。
【分散】
VAR.P→標本を母集団と見なした場合に使用する分散→「標本分散や単に分散」など
VAR.S→標本を元に母集団を推定して使用する分散→「不偏分散」
VARPA→個人的にあまり使わないので後述
VARA→個人的にあまり使わないので後述
※2007以前
VARP→VAR.Pに相当
VAR→VAR.Sに相当
【標準偏差】
STDEV.P→標本を母集団と見なした場合に使用する標準偏差→「標準偏差」
STDEV.S→標本を元に母集団を推定して使用する標準偏差→「標本標準偏差」
STDEVPA→個人的にあまり使わないので後述
STDEVA→個人的にあまり使わないので後述
※2007以前
STDEVP→STDEV.Pに相当
STDEV→STDEV.Sに相当
【共分散】
COVARIANCE.P
COVARIANCE.S
※2007以前
COVAR→COVARIANCE.Sに相当
いかがでしょうか。3種類の指標に対してこんなに細かい計算手法があるとは、あらためて驚かされます。
ただ、規則性があることはお分かりいただけましたでしょうか。
関数のベース名(VAR,STDEV,COVARIANCE)×(母集団Pまたは母集団推定S)+α
この記事では、母集団「P」と母集団推定の「S」の使い分けを説明していきたいと思います。
■母集団と母集団推定の違いは?
便宜上、母集団と母集団推定と先ほどから記載しておりますが、正直わかりづらいですね。
例えば3年B組の成績を評価する際に、母集団は「3年」なのか「3年B組」なのか、という話に書き換えができます。また、母集団推定とは→「観測されたデータ=標本を母集団として扱うかどうか」の話なので以後は「標本」という呼称に変えていきます。
Wikipedia より
統計学における母集団(population)とは、調査対象のとなる数値,属性等の源泉となる集合全体を言う。統計学の目的の一つは、観測データの標本(sample)から母集団の性質を明らかにすることである。
おそらくですが、「母集団=population=P」で、「観測データの標本=sample=S」だと思っているのですが、どうなんでしょうね。違うと思われる方がおりましたらお教え下さい。
上記のように、母集団のデータを完全に集めることはできません。
例えば桜中学校の3年B組だけでなく3年生全員の成績を集めることは、桜中学校長や学年主任がGOといえば集めることができるでしょう。しかし、日本全国の中学3年生全員の成績や、世界中の中学校3年生の成績を集めることは、もう無理! って言ってしまってもいいんじゃないでしょうか。
そんななかで、「標本の計算結果を補正したら母集団と同じような数値になるんじゃない?」と考えた昔の優秀な学者の方々が、標本から母集団を推定するための計算式を発明しました。
それが不偏分散(VAR.S)や標本標準偏差(STDEV.S)や不偏共分散(COVARIANCE.S)となります。
■母集団と標本の計算
過去記事にもあるとおり、
平均=データの合計/データの合計個数
分散=(個別データ-平均)の合計/データの合計個数
標準偏差=分散の平方根
という計算式でした。
実は上記は「データの合計個数=母集団」と見なした場合の計算式になり、標本から母集団を予想(推定)する場合にはデータの合計個数から1を引くという補正を掛けて計算をします。
平均=データの合計/データの合計個数←※これはこのまま
不偏分散=(個別データ-平均)の合計/(データの合計個数-1)
標本標準偏差=分散の平方根
なんで1を引くんだ、という数理的な部分は別の折にご紹介致しますが、エクセルを用いた下記の表をご覧下さい。
DATA①という列でデータに対する各種計算を下部にてしており、その隣DATA①’-1~10の間にてそれぞれのデータから1個ずつ欠損を入れております。
DATA①’-1~10まででそれぞれ欠損を入れた上で下部に計算を行い、最後の列で各値の「平均値」を計算しております。DATA①とDATA①’-1~10は同じデータと言えます。なぜなら9列分のデータを1欠損ずつ出力して10列にしているわけですので、データに対する平均の値も『欠損を計算に加えなければ』同じ結果になることがわかります。
各データで得られた分散や標準偏差の平均は欠損が生じていませんのでそのまま平均を計算していますが、見てお分かりのとおり不偏分散(VAR.S)と標本標準偏差(STDEV.S)に於いて1列目と同じ値になっていることがわかります。
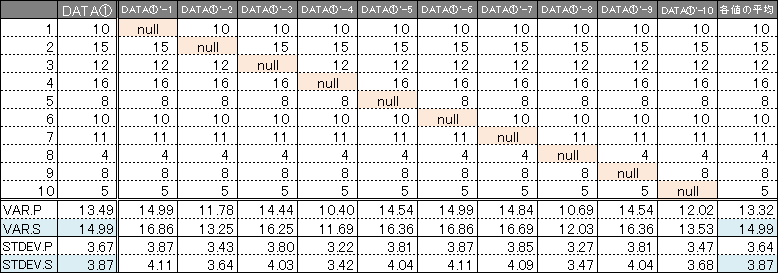
仮に何度も何度も同じデータをとり続けることができるのであれば、不偏分散は標本分散にたどり着く。はずです。これが、それぞれのデータで不偏分散を計算し続けてもた結果がちょっとずつずれていってしまう。可能性がある。といったところでしょうか。したがって統計量を計算する際にはPよりSを使用する方が無難です。
分散、標準偏差、共分散の記事では便宜上「P」を使用しておりました。
■なぜ相関係数(CORREL)にPやSがないのか?
すごく素朴な疑問です。分散や標準偏差、そして共分散を元に計算をする相関係数には、なぜ不偏相関係数(CORREL.P)といったものがないのか。ここまで紹介しているなかで、そんなことを考えたあなたはきっと、めくるめく統計の迷宮に迷いこんでいることでしょう。
答えはまた次回で! というように思わせぶりなことはしません。答えは「そんなものありません」ので。
相関係数の計算方法には大きく分けて2通りあります。
データABに対して
①{(A-平均値A)×(B-平均値B)}の合計/{(A-平均値A)の二乗の合計×(B-平均値B)の二乗の合計}の平方根

②ABの共分散/Aの標準偏差×Bの標準偏差
![]()
①と②の計算では過程が違いますが、どちらも同じ値が出ます。
大まかにいうと個数で割っていない→①、個数で割っている→②になります。
一見すると①が複雑そうに思えますが、①は合計と平均と少々の平方根で構成されていることに対して、
②は簡単に見えますが共分散や標準偏差(V=分散)が登場してくるので①に比べ計算過程が難しいです。
また、①のとおり「個数で割っていなくとも」計算ができる点がポイントです。相関係数は個数で割らなくても計算できるため、逆に言えばどんな数値で割ろうとも答えが同じになるのです。
例{(A-平均値A)×(B-平均値B)}の合計×10/{(A-平均値A)の二乗の合計×(B-平均値B)の二乗の合計}の平方根×10
![]()
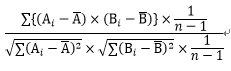
なんとなくイメージがつきましたでしょうか。
※当然のことですが分子にも分母にも同じ数値を掛けて下さい。
■分散の関数VARPA、VARA及び標準偏差の関数STDEVPA、STDEVについて
前述のとおり、私(筆者)は使ったことがありません。
ということでこの記事を書くにあたり調べたところ、関数使用時に下記のような説明が出ておりました。
「論理値や文字列を含む引数を計算対象と見なして結果を返します。文字列及び論理値FALSEは0、論理値TRUEは1と見なされます。」
ということで、下記のようなデータの場合に、FALSEは0、TRUEは1として計算するそうです。

使い道を探そうとすればもちろん十分ありそうですが、べつになくてもいいんじゃないでしょうか…きっとそれは、私のエクセルスキルの低さが所以ではないかと…。