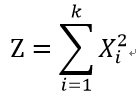正規分布について｜Excel（エクセル）で学ぶデータ分析ブログ

■正規分布とは？

Wikipedia より(一部編集)
“確率論や統計学で用いられる正規分布（Normal distribution）またはガウス分布（Gaussian distribution）は、平均値の付近に集積するようなデータの分布を表した連続的な変数に関する確率分布である。中心極限定理により、独立な多数の因子の和として表される確率変数は正規分布に従う。このことにより正規分布は統計学や自然科学、社会科学の様々な場面で複雑な現象を簡単に表すモデルとして用いられている。たとえば実験における測定の誤差は正規分布に従って分布すると仮定され、不確かさの評価が計算されている。”

正規分布は確率分布の王道的な存在といっても過言ではありません。
様々な確率分布が加工の仕方によって正規分布で近似することになり、分析の際に非常に強力なツールとなります。

数式はこんな感じ。

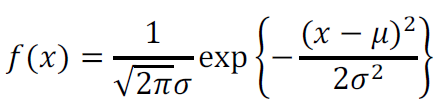
統計の本を読むと必ず登場する数式ですので、見たことがある、という方は多いと思います。
しかしながら、「意味を理解」しようとすると、途端に冷や汗、悪寒、微熱におそわれ、次いで呼吸困難、腹痛を経て本を閉じてまた今度！　ということになることは必定といえます。
筆者もアラサーを迎えてからの独学でしたので苦労したことを覚えております。

それでも、理解してしまうとこんなに便利で秀逸な数式もないな、と感じてしまうところが正規分布の素晴らしいところ。
この当ブログでは極力数理的な点を扱わないようにしておりますので、さらっと、麦茶でも飲むように読み流していただければと思います。

---

■正規分布の使い方

ポイントは下記の３点
x = 対象となる値
μ = 平均値
σ =　標準偏差

エクセルの場合は「x = 8、μ =5、σ =　2」とすれば
【1/(SQRT(2*PI())*2)*EXP((-1)*(8-5)^2/(2*2^2)) =0.0648】となります。

図示すると下記の表とグラフになります。

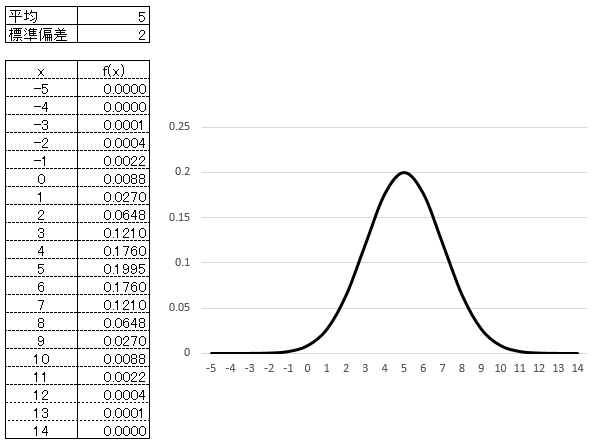
5の値を中心(平均)に、左右へ山型に値が広がっています。
見た目には二項分布と似ていますが、二項分布が「試行回数と比率」で計算されていたのに対して、
正規分布は「平均値と標準偏差」で計算されることを覚えておいてください。

続いて正規分布の式をちょっとだけ加工します。

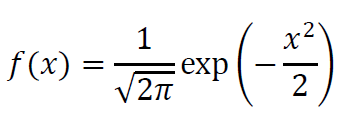
前述の数式とくらべ、ちょっとスッキリしたと思いませんか？
まず、平均値(μ)を0に、標準偏差(σ)を1にすると、xの値だけで正規分布の計算ができます。
こちらの式は標準正規分布と呼ばれています。

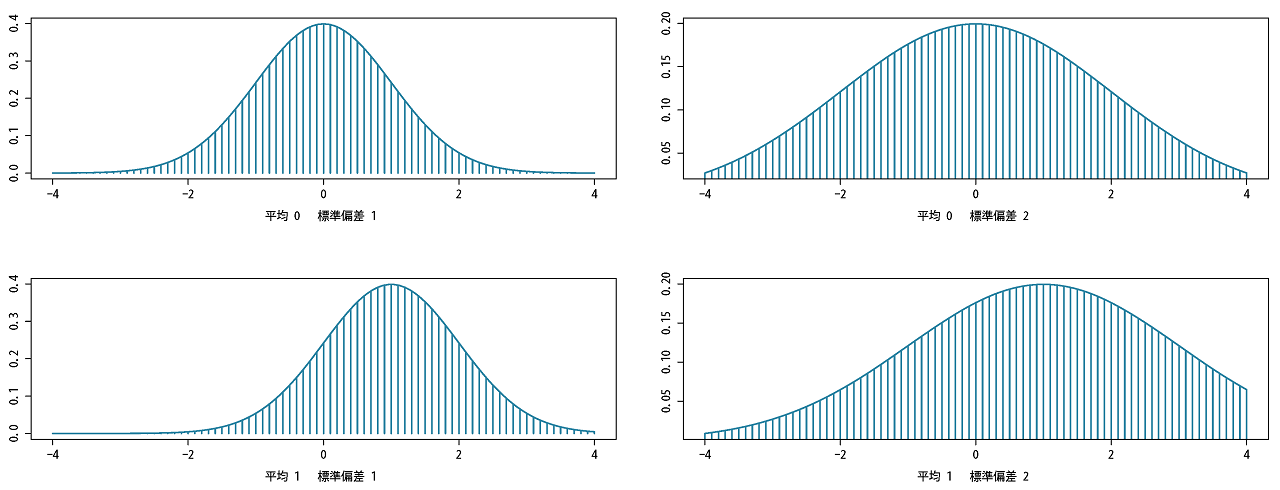
上段：左：平均0・標準偏差1　右：平均0・標準偏差2
下段：左：平均1・標準偏差1　右：平均1・標準偏差2
左上の図が標準正規分布で、標準偏差が増えれば山がボワ～ンと広がって、
平均値が増えると右へ並行移動することがわかります。

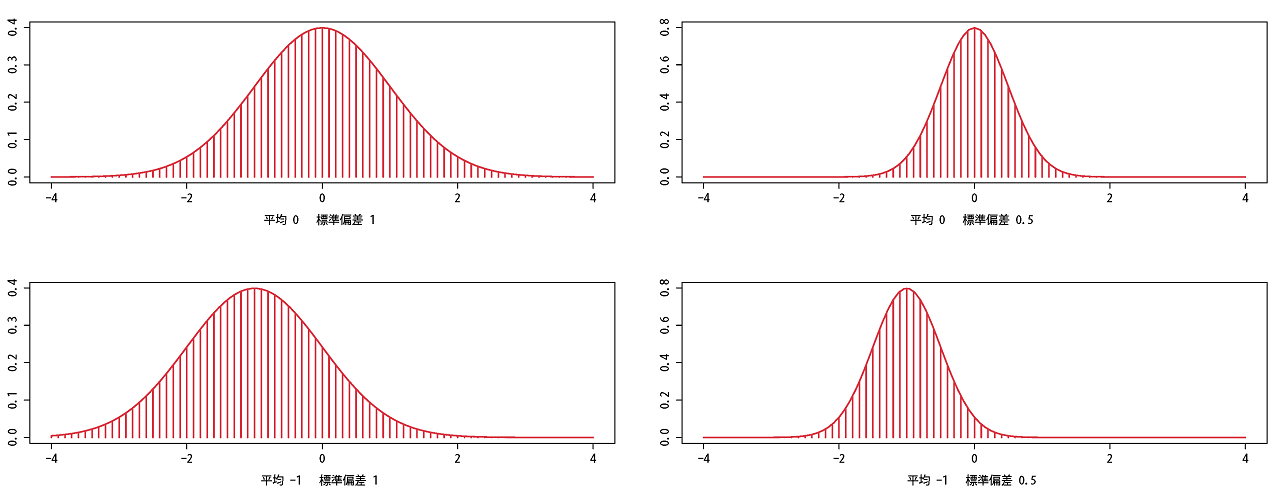
上段：左：平均0・標準偏差1　右：平均0・標準偏差0.5
下段：左：平均1・標準偏差-1　右：平均-1・標準偏差0.5
逆に、標準偏差が減ればキュイ～ンと狭くなり、
平均値が減ると左へ並行移動することがわかります。

また、標準偏差の記事で「±標準偏差の値の間にほとんどの値が含まれている」という説明をしましたが、
データの分布を正規分布と過程した場合、厳密には
±σ×1の範囲=68.27%
±σ×2の範囲=95.45%
±σ×3の範囲=99.73%
のデータが含まれていることになります。

ということでシミュレーションして確認してみましょう。

---

■正規分布内の標準偏差の範囲

まずは、標準正規分布に沿う乱数を100,000個出力します。

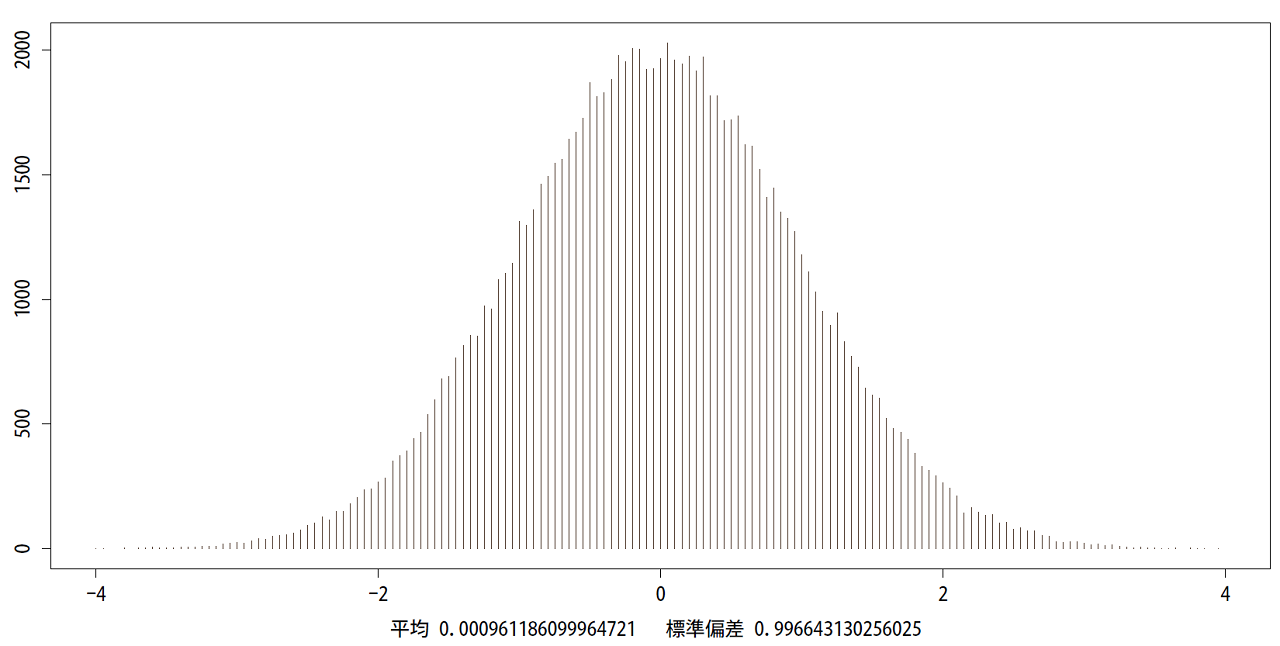
近似した乱数なのでまったく同じ平均、標準偏差には収まりませんが、及第点としましょう。
σ×1＝0.9966431
σ×2＝1.993286
σ×3＝2.989929
となりますので、それに合わせて計算をしたところ下記のとおりの結果となりました。

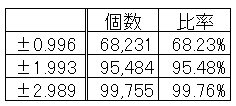
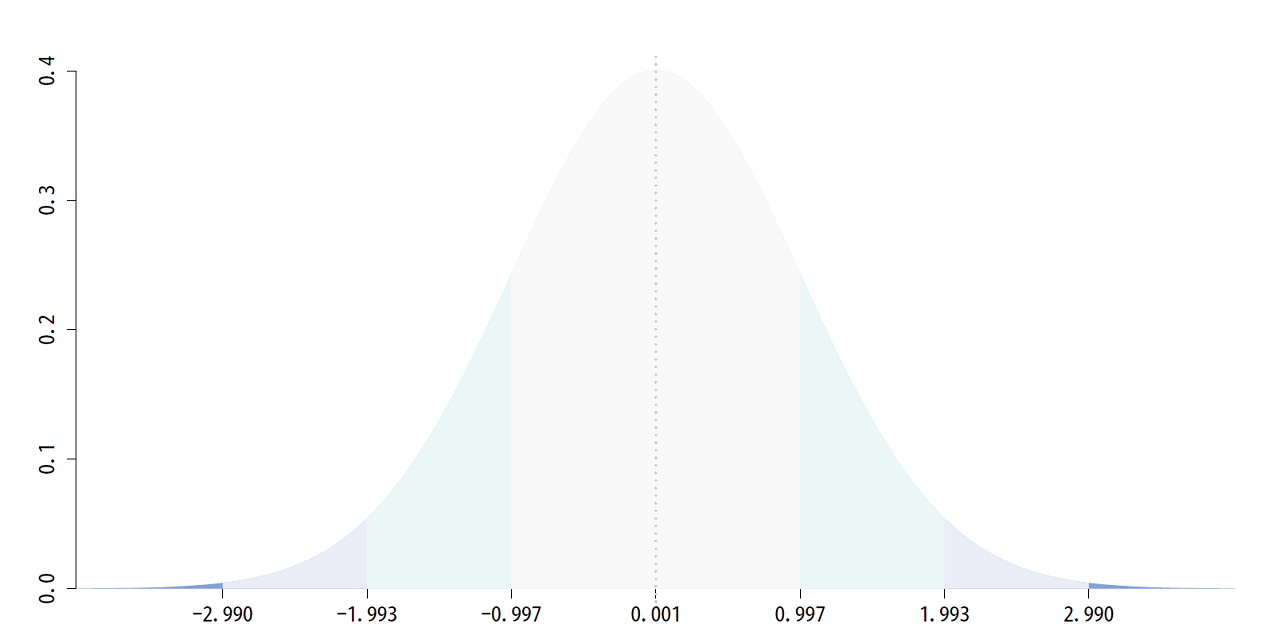
統計の検定や推定という手法では、この「範囲」という考え方、手法に対する理解が必須となってきます。