順位和検定について｜Excel（エクセル）で学ぶデータ分析ブログ
順位和検定とは
順位和検定（ウィルコクソンの順位和検定／マン・ホイットニーのU検定）はノンパラメトリックな統計学的検定の一つであり、特に特定の母集団がもう一方よりも大きな値を持つ傾向にある時に、2つの母集団が同じであるとする帰無仮説に基づいて検定する。
順位和検定の説明(概要)
よくt検定の代替として使われるケースが多く、使いどころとしては 「正規性が確信できない」場合などに使用されます。
この「正規性が確信できない」という点は解釈が難しいため下記のような分布を作成しました。
何れも正規性検定(シャピロ–ウィルク検定)では限りなくゼロに近い数値となっています。
こういったデータが2群与えられた場合にそのまま「正規性を前提としたパラメトリックな検定」に掛けた場合、正しく検知されるのか、いやされないだろう、ということで順位和検定を用います。
サンプルデータを作成する
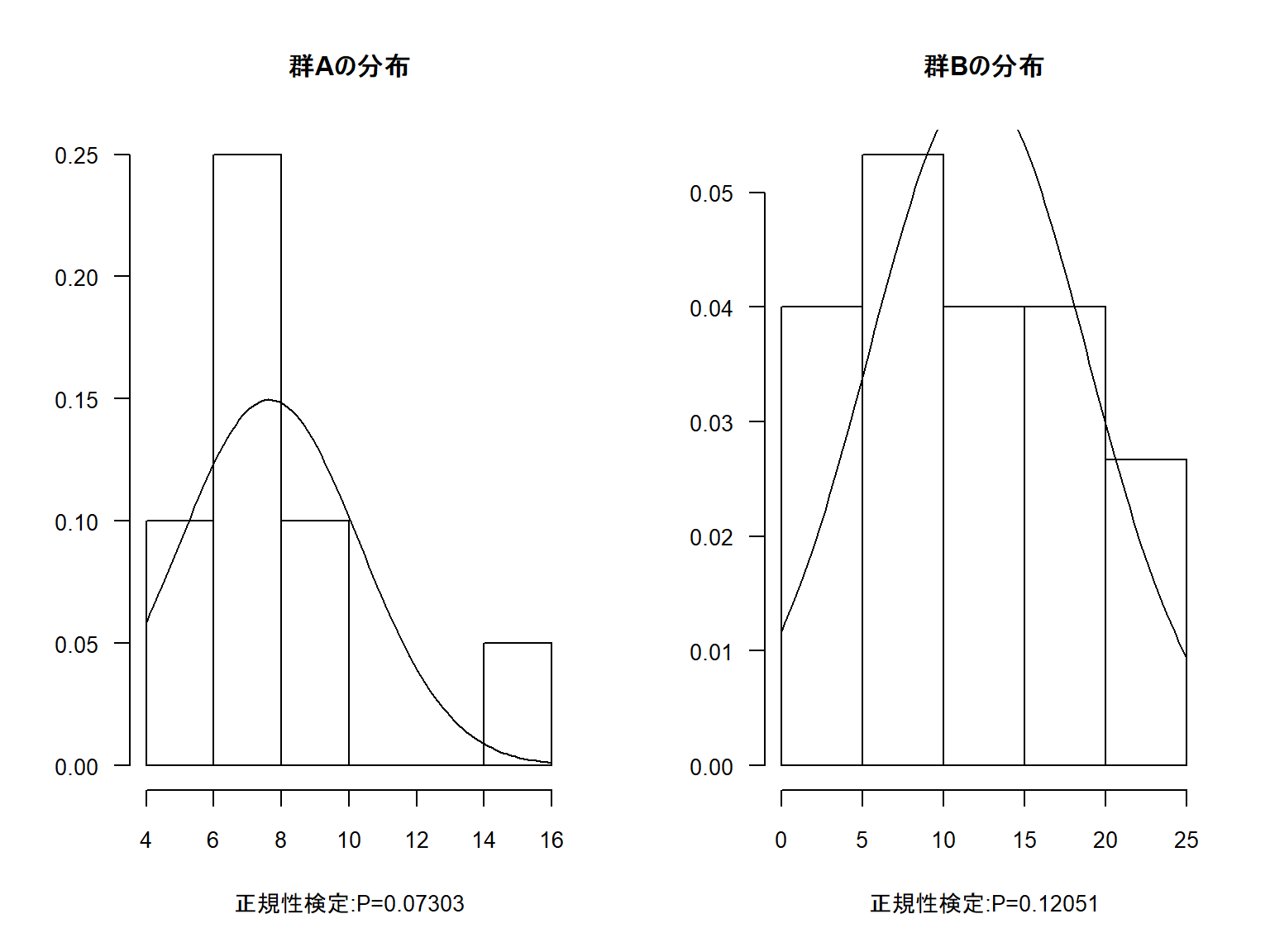
例えば下記表のようなデータがあったとします。
順位和検定用元データ
このデータをt検定に掛けた結果は下記のとおり0.05を水準として有意な差となりました。
t検定の手順は他記事を参考ください。
| t統計量 | 自由度 | P値 | 比較法 |
|---|---|---|---|
| -2.311 | 19.69 | 0.03177 * | 両側検定 |
説明に都合の良い乱数が見つからなかったので
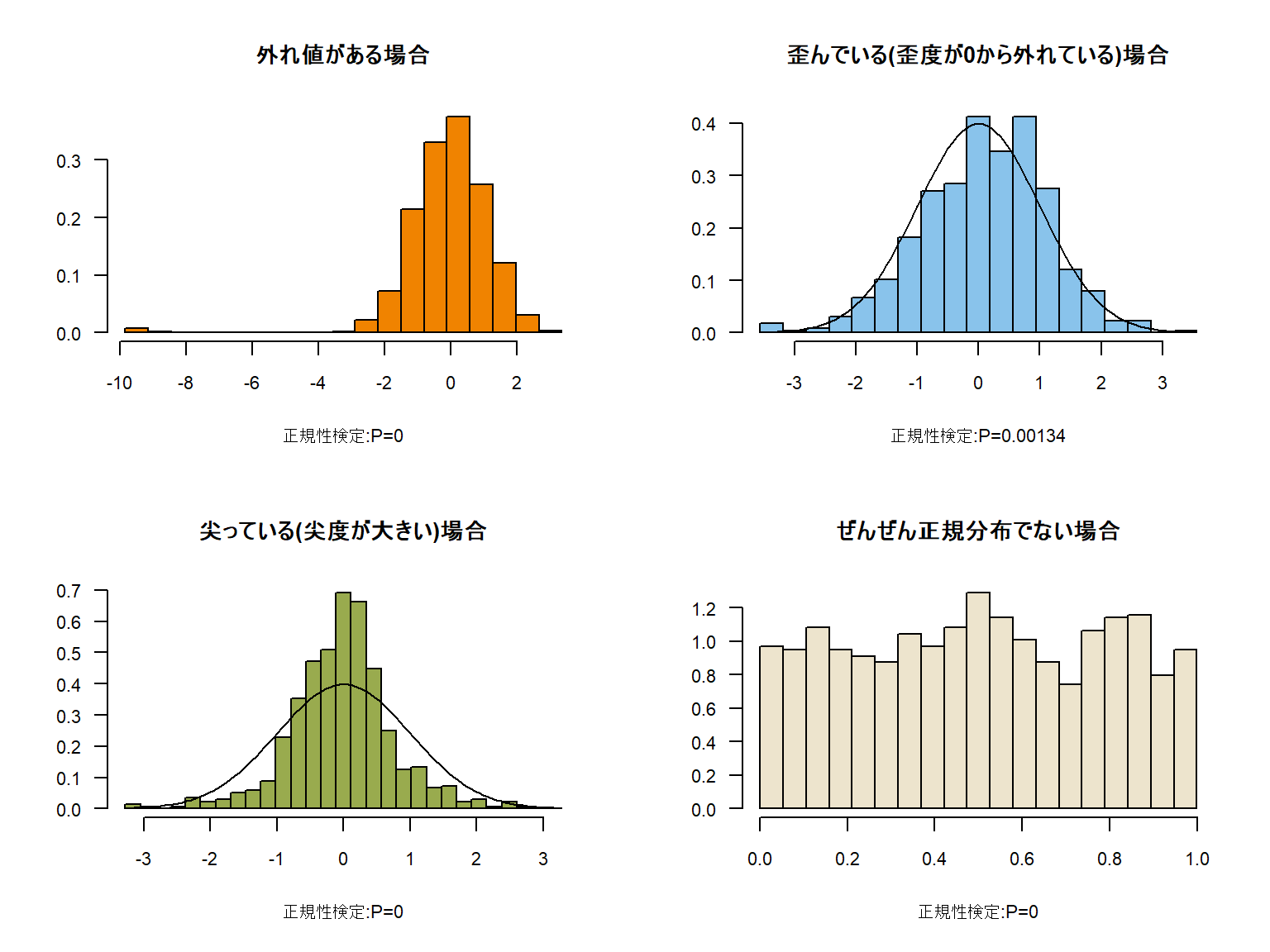
正規性検定の結果は有意水準0.05で棄却できないもののグラフを見た感じでは微妙な気がします。
ということで、順位和検定を行います。
手順は下記のとおりです。
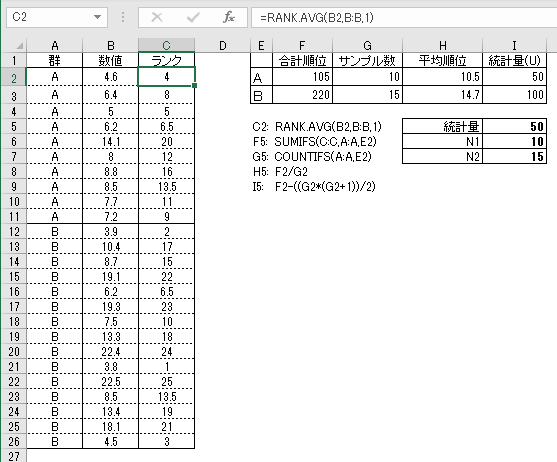
①群AとBを合体させて数値の順位を算出する
②順位が同じ(タイ)のときは「順位の間」の数値とする
例1:6位と7位が同じ数値=どちらの順位も「6.5」とする【(6+7)/2】
例2:6位と7位と8位が同じ数値=どの順位も「7」とする【(6+7+8)/3】
※エクセルの場合はRank.AVG関数で簡単に計算ができます。
③それぞれの群れの順位を合計し「合計順位」を算出する
④合計順位から「サンプル数×(サンプル数 + 1)／2」した数値を引く
※なぜそうするかは別記事にて説明します。
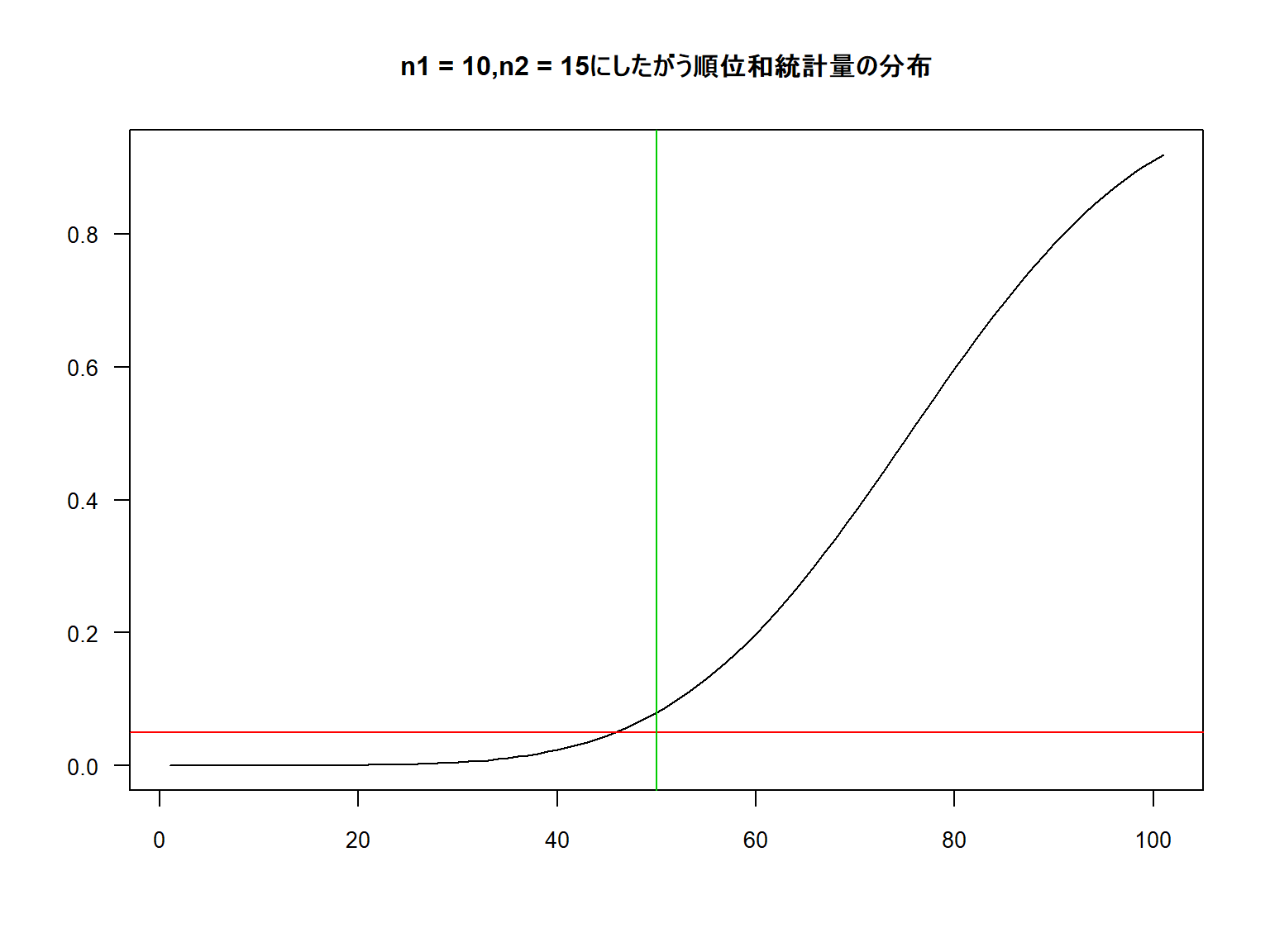
⑤④のk結果を順位和統計量の分布と比較して確率を計算、評価する。
算出された統計量は「50」で、これはN1 = 10,N2 = 15にしたがう順位和統計量分布のなかでの
発生率は「0.0087」となり両側考慮した場合は「0.174」となります。
| 統計量 | P値 | 比較法 |
|---|---|---|
| 50 | 0.174 | 両側検定 |
この結果はt検定の結果と順位和検定の結果が明らかに乖離しているケースを紹介するために「あえて」取り出した数値です。
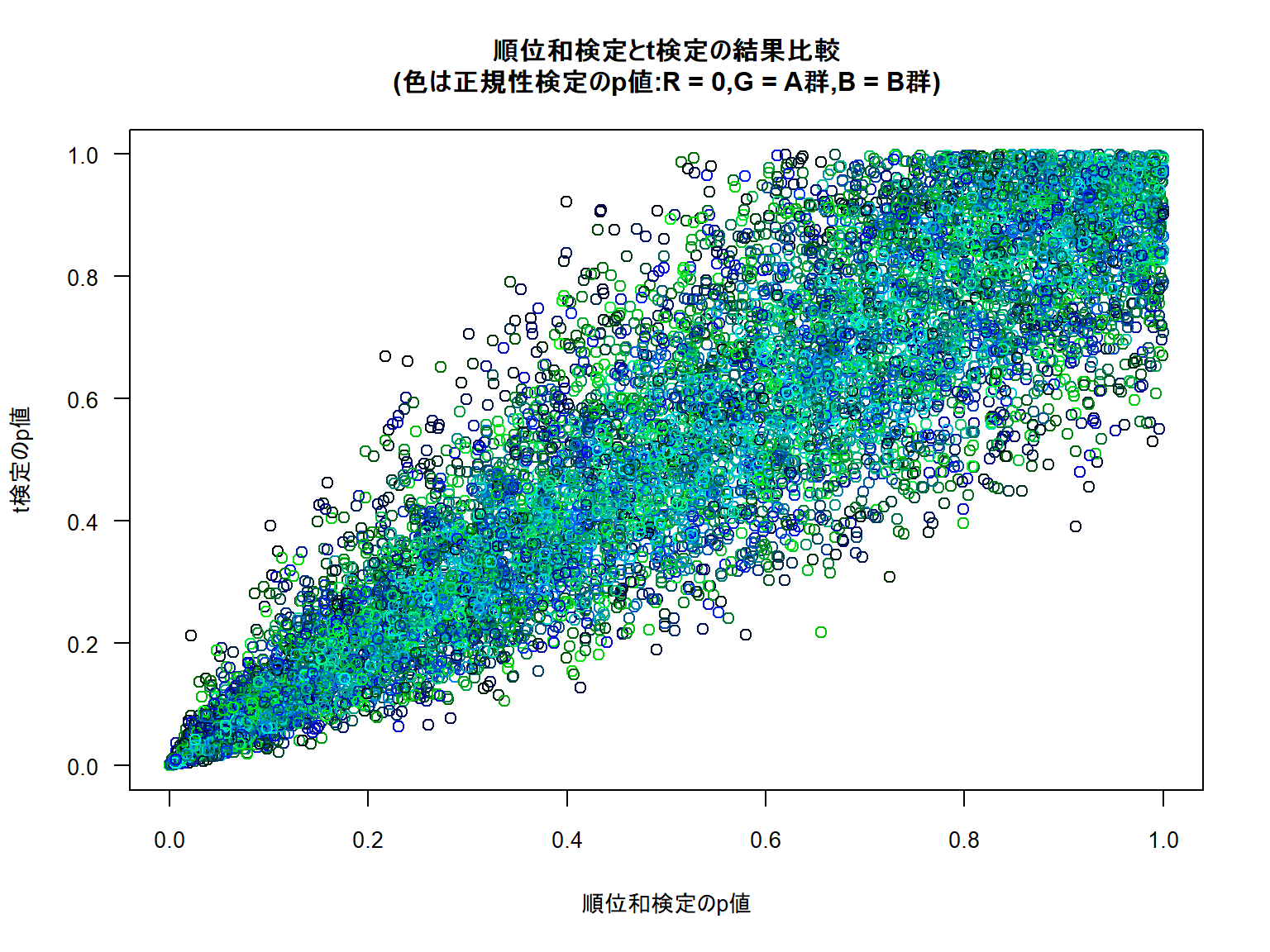
通常は下記の図のようにt検定の結果と順位和検定の結果は似たような結果となります。
観察してみると、正規性が確信できない分布の場合にはそれぞれの検定による結果にばらつきがあるように感じます。
これらの説明はまた別の機会に。
