ざっくり読み解く 主成分分析
はじめに
多変量解析と言えば最初に思い浮かべるのが主成分分析ではないかと個人的には考えます。
主成分分析は【principal component analysis】略して「PCA」などとも呼ばれており、初学者にとっては最初に心が折れる要衝とも言えます。
仕掛けとしては固有値計算をするだけなのですが、そもそも固有値ってなんぞ? ってところで筆者も苦しみました。
感覚的に把握してもらえるよう、まとめていきます。
目的と使いどころ
アンケートで「1:まったく思わない⇔5:たいへん思う」などの5件法で10問くらい取ったことがあれば、情報を俯瞰して見たくなるシーンがあると思います。
そんなとき、とりあえずどこから手をつけたらいいか、という取っ掛かりとして主成分分析をかけ
なるほどなーとフムフムするわけです。
俯瞰して見るというものを、言葉通りに読み解くと「高いところから見下ろす」ということです。
高いところから見下ろすと、どういうことが起きるのか
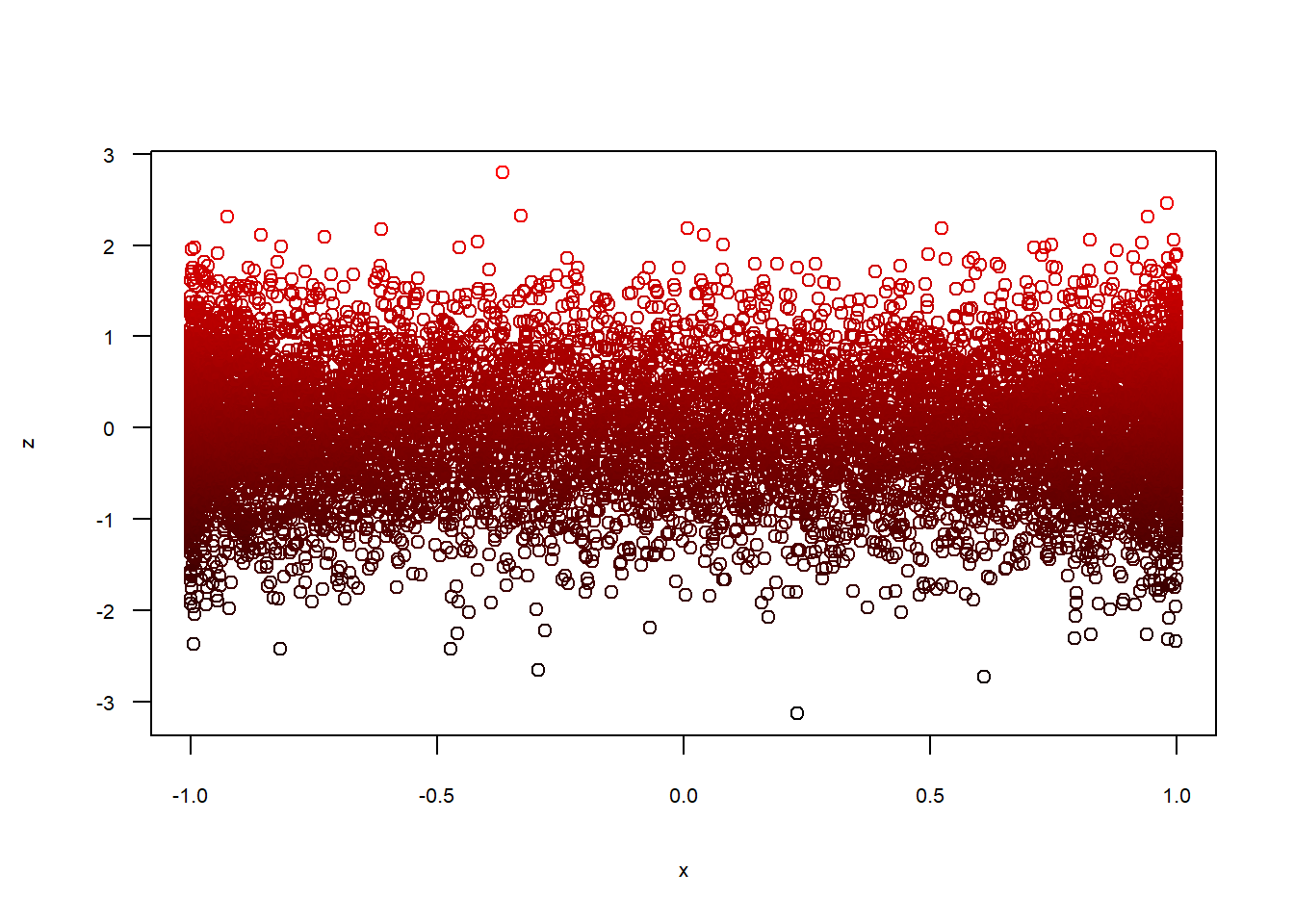
例えばこのような2次元散布図はどうなるのか。
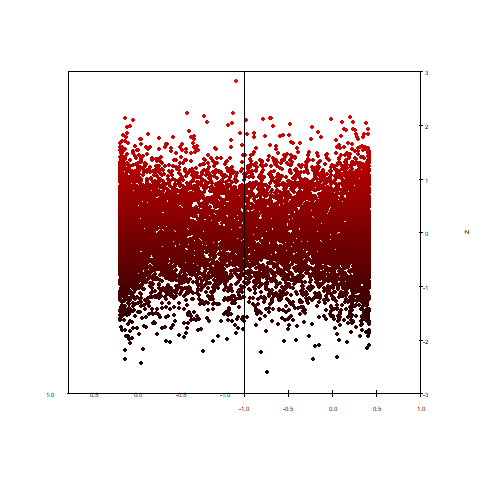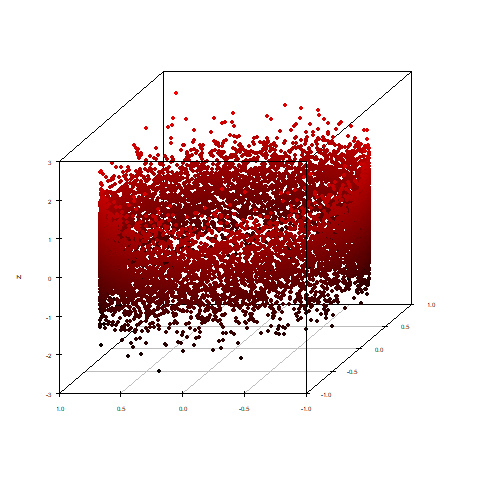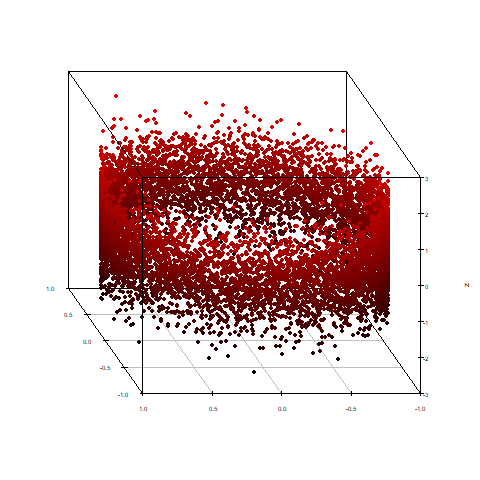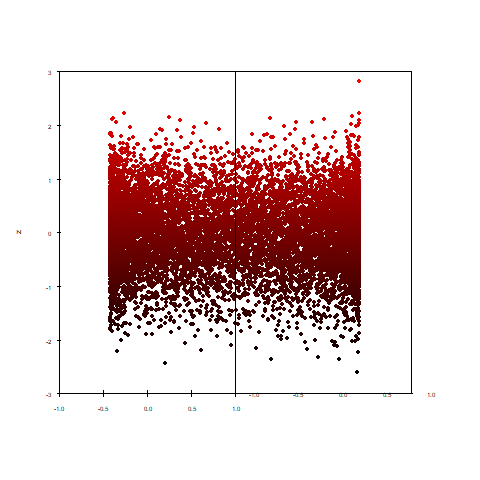
2次元で捉えるとランダムな散布図のように見えるものでも、見える角度によってそれが円であることがわかりました。
真上から見た図です。
今回のサンプルデータはxy軸に円を、z軸に正規分布の乱数10,000個を加えた3次元データになります。
次元を圧縮しても残る情報
例えばフルーツジュースを考えます。
季節に合わせて適当に5種ほどミキサーに入れたとします。
なんとも言えないフルーツの味がすると思いますが、その中にもバナナっぽさやりんごっぽさを感じるはずです。
ざっくり言えば、主成分分析はそのフルーツジュースのようなものだとイメージしてください。
これをちょっと難しい表現で言えば次元を圧縮する、といいます。
今回のデータで言えば3次元のデータを「極力3次元らしさを残しながら2次元や1次元に圧縮する」処理法です。
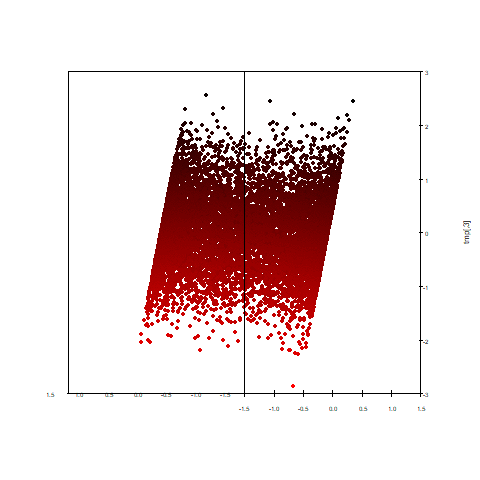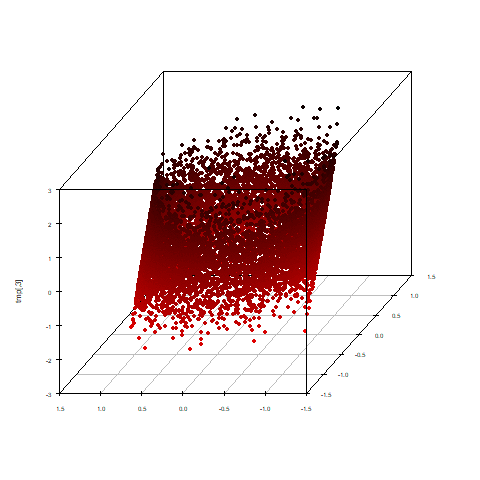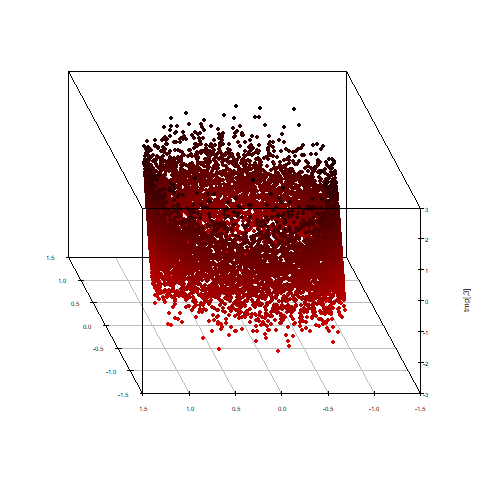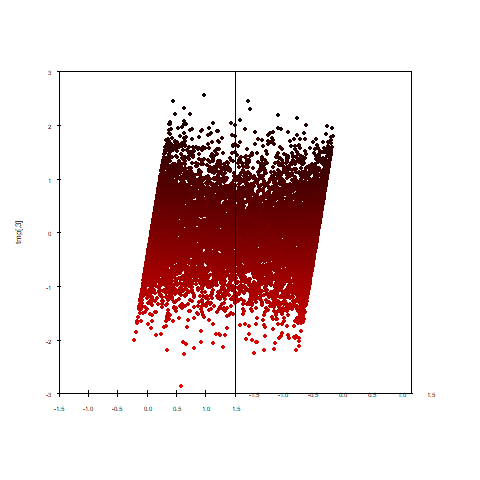
こちらが今回使用したデータへ主成分分析を掛け、第1・2主成分得点を散布図にしたものです。
円の形を残しながら、z軸で与えられたランダムな情報が残り、先程のアニメーションのように「斜めから見た」ような図になりました。
先ほどと同じようにアニメーションにしてみました。
x:第1、y:第2、z:第3主成分得点を立体散布図にすると、少しギュイーンとした感じはありますが
元の形を残しています。
非常にざっくりとした解説ですが主成分分析をイメージできましたでしょうか。
より詳しいことを知りたい場合は「主成分分析 詳しく」などで検索してみてください。
当ブログでも、需要があれば詳しく説明するバージョンも作ろうと思います。
関連しそうなキーワード:主成分負荷量、主成分ベクトル、主成分得点、固有値、相関係数