ざっくり読み解く 重回帰分析
はじめに
いわゆる多変量解析の中でも、最も実用的なものは重回帰分析だと思います。
それはデータを「目的(従属)変数」と「説明(独立)変数」とに分離させ、
目的変数に対する影響力を示してくれるからです。
目的と使いどころ
具体的には
\[
y(目的変数) = a(回帰係数) X(説明変数) + b(切片)
\]
という形にデータを分けてくれるということです。
※説明しやすさを優先し\(b(切片)\)は「ほぼ0」として進めます。
アルファベットだとちょっとわかりにくいので、
例えば筆者がホテルのマーケティング担当で
ホテルの満足度を分析し数式化させることに成功したとします。
そしてそのモデルを下記のように定式化したとします。
\[
ホテルの満足度 = 1.5 \times 快適さ + 1.2 \times 料理の質 -0.5 \times 宿泊料金
\]
つまるところ(ざっくり言えば)快適さと料理の質を追求すればより満足度に貢献し、
且つ宿泊料金を抑えることでより高い満足度を得られるのだということです。
それは過去利用いただいた5,000人のお客様のアンケートから得た知見です。
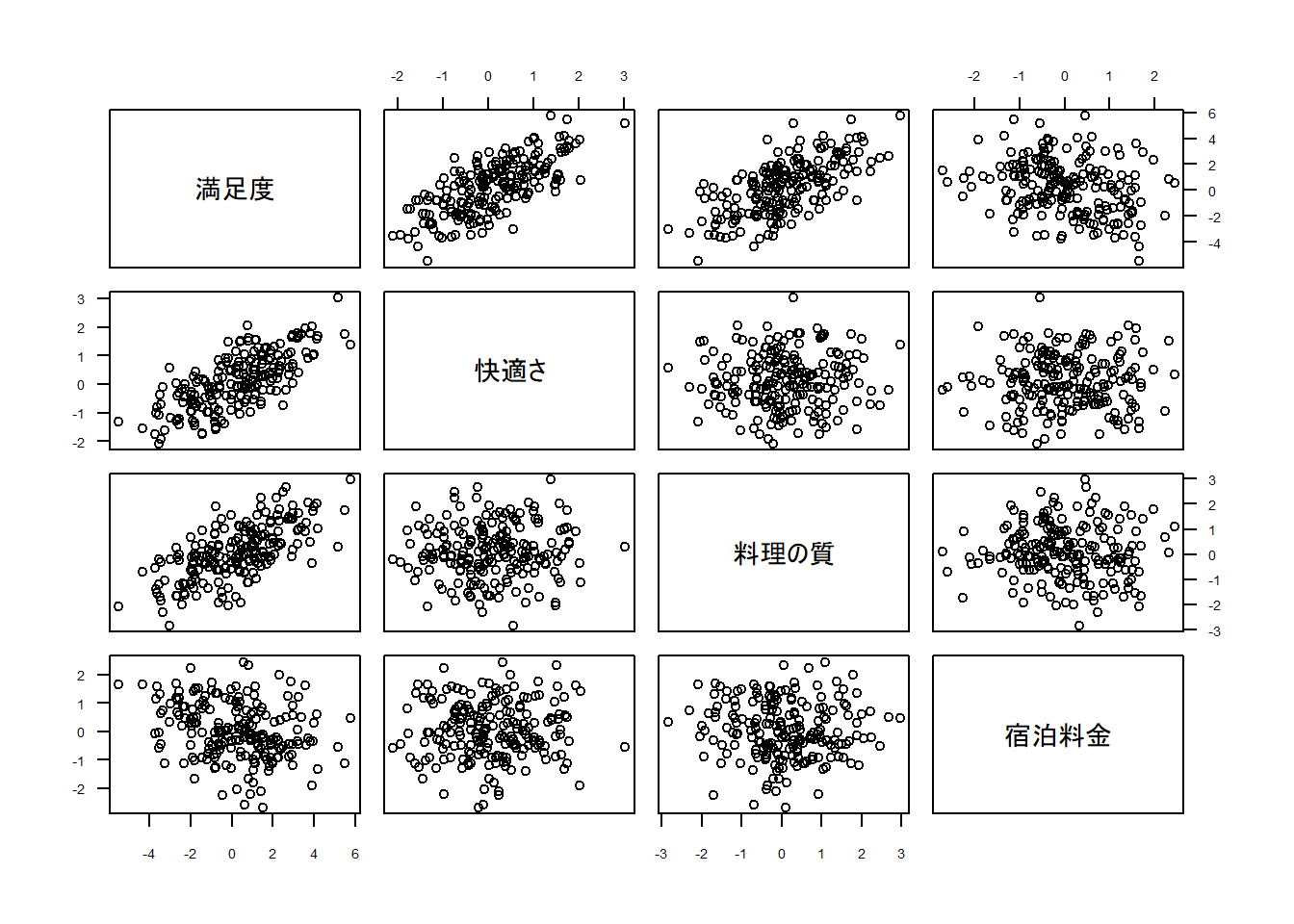
散布図行列は全部出力するとよくわからなくなるので200ほどランダムに抜き出したものを図示しました。
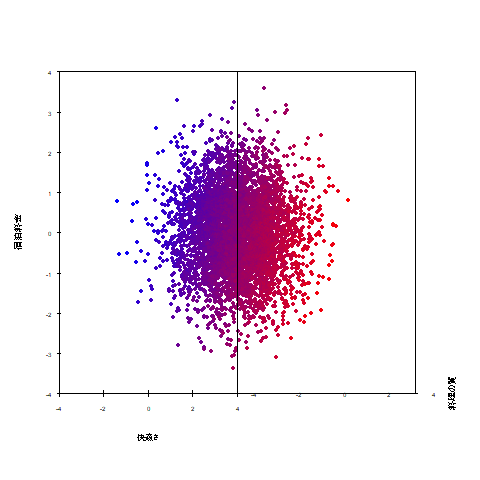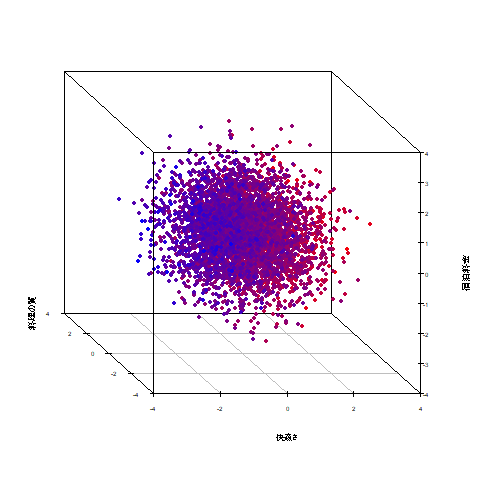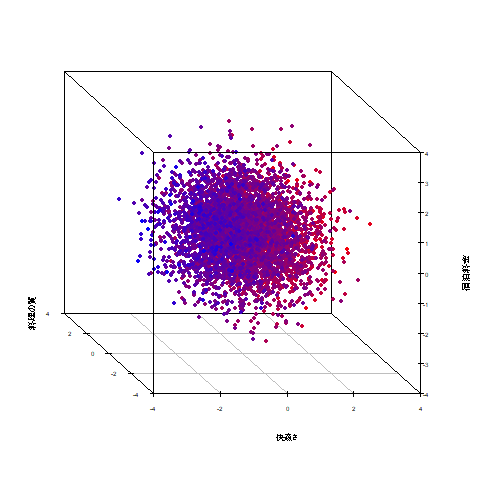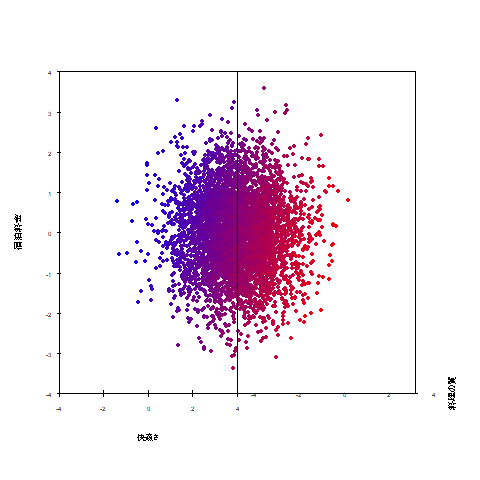
快適さ×料理の質×宿泊料金の3次元に、赤いほど満足度が高く、
青いほど満足度が低いという色の情報を加えることで3次元プロットで4次元の情報を表現しました。
快適さ、料理の質に評価が高く、宿泊料金を低いと感じている利用者ほど赤く、
逆の感想を抱いた利用者ほど色味が青くなることが確認できます。
※宿泊料金は高いと感じた人ほど満足度が下がるため、斜め下方向が最も赤い。
つまるところ、快適さを追求し、料理の質も高めながら、宿泊料金を抑えてご提供する、ということですね。
当たり前のような気もしますが、5000人の利用者から得た知見となればかなり信頼性がありそうです。
重回帰分析の導出
使用データの共分散行列を図示します。
| 満足度 | 快適さ | 料理の質 | 宿泊料金 | |
|---|---|---|---|---|
| 満足度 | 4.05 | 1.52 | 1.19 | -0.52 |
| 快適さ | 1.52 | 1.02 | 0 | -0.01 |
| 料理の質 | 1.19 | 0 | 0.99 | 0.01 |
| 宿泊料金 | -0.52 | -0.01 | 0.01 | 1.02 |
先ほどの散布図行列同様、各変数間は無相関で満足度との高い相関性が窺えます。
この各関係性を元に連立方程式を組み、係数(a)を導出します。
\[
\begin{array}{l}
満足度(y) = a_1 快適さ(x_1) + a_2 料理の質(x_2) + a_3 宿泊料金(x_3)\\
\\
\begin{array}{|c|}
\hline
満足度(y)\\
\hline
1.52 \\
\hline
1.19 \\
\hline
-0.52 \\
\hline
\end{array}
~=~
\begin{array}{|l|l|l|}
\hline
快適さ(x_1) & 料理の質(x_2) & 宿泊料金(x_3)\\
\hline
a_1 \times 1.02 & a_2 \times 0 & a_3 \times -0.01\\
\hline
a_1 \times 0 & a_2 \times 0.99 & a_3 \times 0.01\\
\hline
a_1 \times -0.01 & a_2 \times 0.01 & a_3 \times 1.02\\
\hline
\end{array}
\end{array}
\]
逆行列を計算すれば係数を得られます。
| 快適さ | 料理の質 | 宿泊料金 |
|---|---|---|
| 1.496 | 1.205 | -0.501 |
収集したデータからは下記のようなモデルになりました。
\[
\begin{array}{l}
ホテルの満足度 &=& 1.5 \times 快適さ &+& 1.2 \times 料理の質 &-0.5 \times 宿泊料金\\
ホテルの満足度 &=& 1.496 \times 快適さ &+& 1.205 \times 料理の質 & -0.501 \times 宿泊料金
\end{array}
\]
重回帰分析を使いこなすには
重回帰分析は他にもその結果が信頼できるものか評価するため
いくつかの諸情報がありますが、それらは「重回帰分析 詳しく」などで検索すると いろいろ出てくると思います。
最低限、下表のような情報が得られ、フムフムできれば重回帰分析は使いこなせているのではないでしょうか。
| Estimate | Std. Error | t value | Pr(>|t|) | |
|---|---|---|---|---|
| (Intercept) | -0.0002981 | 0.004105 | -0.07262 | 0.9421 |
| 快適さ | 1.496 | 0.004069 | 367.7 | 0 |
| 料理の質 | 1.205 | 0.004122 | 292.3 | 0 |
| 宿泊料金 | -0.5008 | 0.004062 | -123.3 | 0 |
| Observations | Residual Std. Error | \(R^2\) | Adjusted \(R^2\) |
|---|---|---|---|
| 5000 | 0.2902 | 0.9792 | 0.9792 |
最初に述べたとおり重回帰分析は実用性が非常に高く
今回用いたような単純な直線をモデル化したものに留まらず
n次方程式のものや正規分布をそのまま適用できないケースなど 本当に奥の深い分析手法です。
このあたりも、また需要があれば記事を作成していこうと思います。
関連しそうなキーワード:偏回帰係数、一般化線形モデル、機械学習、ロジスティック回帰分析、多重共線性(マルチコ)