ざっくり読み解く 主成分分析【もうちょっと詳しく編】
はじめに
主成分分析の話題。
主成分分析は固有値と固有ベクトルを計算して
固有ベクトルをちょっと加工して主成分負荷量
固有値と固有ベクトルをちょっと加工して主成分得点などを計算し傾向などを分析します。
固有値や固有ベクトルってなんですの?
ということで、下記のような関係性をご紹介。
\[
\begin{array}{l}
Ax = \lambda x\\
\begin{array}{l}
A &=& 対象の行列&:&共分散行列や相関行列など\\
\lambda &=& 固有値&:&加工して累積寄与率などを計算\\
x &=& 固有ベクトル&:&ちょっと加工して主成分負荷量と呼ぶ
\end{array}
\end{array}
\]
固有値、固有ベクトルの計算は3行3列で整数のときなどは
手計算でもなんとかなります。
しかし10行10列の相関行列などから同じような計算はとても大変です。
そのため様々な計算手法が編み出され
わかりやすいもの、計算効率が良いものなど
ひとつずつ理解するだけで途方も無い時間がかかります。
今回は代表的なものをざっくりとご紹介します。
使用した相関行列
| v_1 | v_2 | v_3 | v_4 | v_5 | v_6 | |
|---|---|---|---|---|---|---|
| v_1 | 1 | 0.755 | 0.699 | 0.771 | -0.303 | -0.214 |
| v_2 | 0.755 | 1 | 0.314 | 0.297 | -0.141 | -0.153 |
| v_3 | 0.699 | 0.314 | 1 | 0.928 | -0.252 | -0.224 |
| v_4 | 0.771 | 0.297 | 0.928 | 1 | -0.396 | -0.26 |
| v_5 | -0.303 | -0.141 | -0.252 | -0.396 | 1 | 0.85 |
| v_6 | -0.214 | -0.153 | -0.224 | -0.26 | 0.85 | 1 |
べき乗法
\[
x^k = Ax^{k-1}
\]
ざっくり説明すると、もとの行列に固有ベクトルをかけ合わせたら
より正確な固有ベクトルに寄っていくんじゃない?
という手法です。
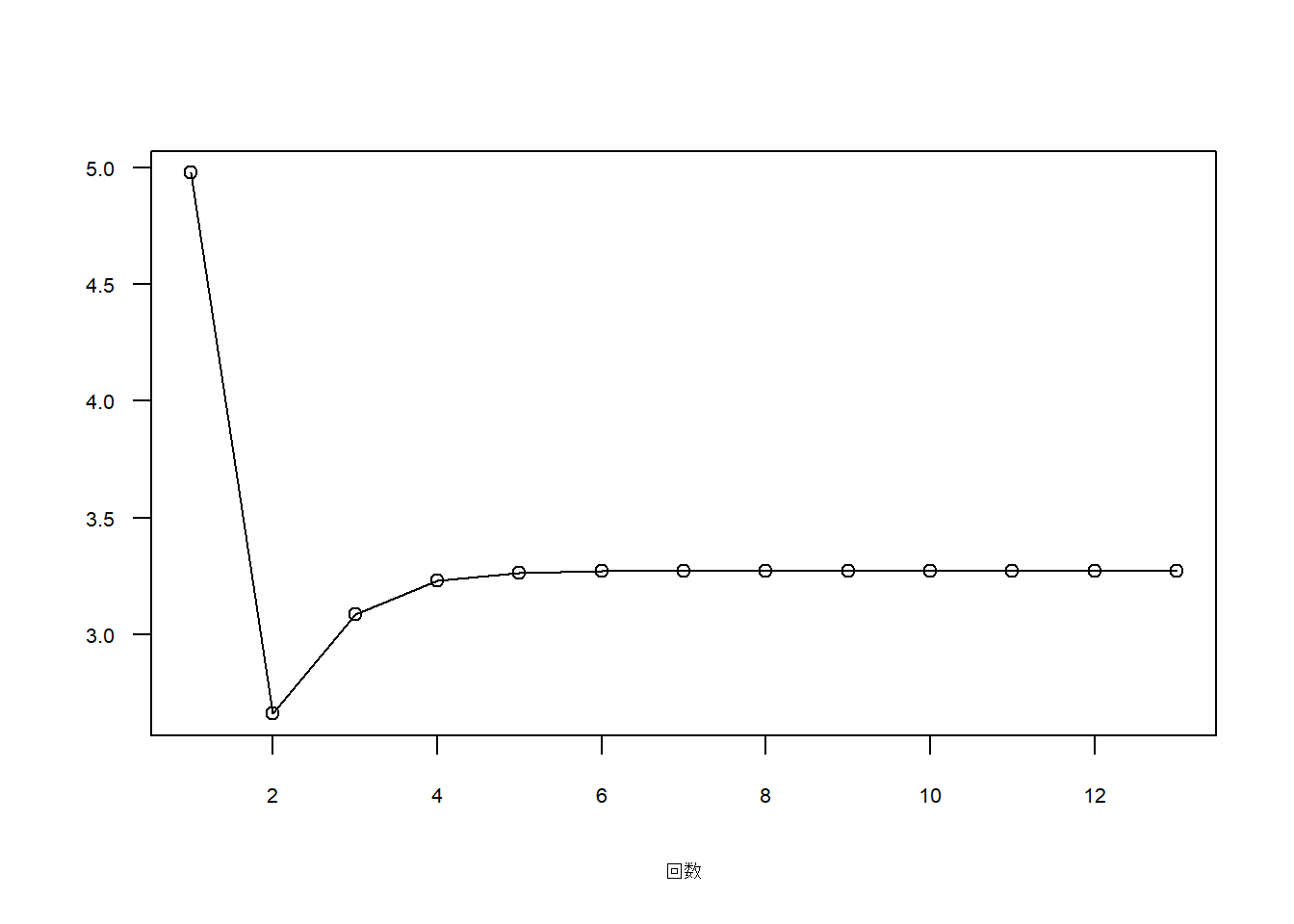
上記の数式を参考に計算が収束するまで繰り返した結果です。
最初の図は固有値、2つめが固有ベクトルが収束する推移です。
繰り返し回数は15回程度でした。
| 手作業 | PRG |
|---|---|
| 0.4901 | -0.4901 |
| 0.3312 | -0.3311 |
| 0.4621 | -0.4621 |
| 0.4896 | -0.4896 |
| -0.3322 | 0.3323 |
| -0.2941 | 0.2942 |
こちらは手作業で値が収束するまで処理した第一主成分ベクトルと
とある(しっかりとした)計算プログラムを使用した結果です。
だいたい合ってますね。ざっくりなので十分です。
下記は固有値の比較です。
| v_1 | v_2 | v_3 | v_4 | v_5 | v_6 | |
|---|---|---|---|---|---|---|
| 手作業 | 3.274 | 1.517 | 0.908 | 0.1934 | 0.08504 | 0.02315 |
| PRG | 3.274 | 1.517 | 0.908 | 0.1934 | 0.08504 | 0.02315 |
固有ベクトル(とあるちゃんとしたプログラム)
| v_1 | v_2 | v_3 | v_4 | v_5 | v_6 | |
|---|---|---|---|---|---|---|
| c_1 | -0.4901 | 0.2713 | -0.2235 | 0.3266 | -0.6205 | 0.3802 |
| c_2 | -0.3311 | 0.258 | -0.7553 | -0.1905 | 0.4038 | -0.2323 |
| c_3 | -0.4621 | 0.2174 | 0.4347 | -0.4717 | 0.3382 | 0.4619 |
| c_4 | -0.4896 | 0.151 | 0.4194 | 0.2167 | -0.0237 | -0.717 |
| c_5 | 0.3323 | 0.6107 | 0.0381 | -0.5327 | -0.4262 | -0.2229 |
| c_6 | 0.2942 | 0.6455 | 0.1153 | 0.5511 | 0.3941 | 0.1561 |
検算
| v_1 | v_2 | v_3 | v_4 | v_5 | v_6 | |
|---|---|---|---|---|---|---|
| v_1 | 0 | 0 | 0 | 0 | 0 | 0 |
| v_2 | 0 | 0 | 0 | 0 | 0 | 0 |
| v_3 | 0 | 0 | 0 | 0 | 0 | 0 |
| v_4 | 0 | 0 | 0 | 0 | 0 | 0 |
| v_5 | 0 | 0 | 0 | 0 | 0 | 0 |
| v_6 | 0 | 0 | 0 | 0 | 0 | 0 |
0ばっかり! と思いますが
これは下記の数式でちゃんと計算できているか比較した表です。
\[
\begin{array}{l}
A = X \Lambda X^{-1}\\
\begin{array}{l}
A &=& 対象の行列\\
\Lambda &=& 固有値*単位行列したもの\\
X &=& 固有ベクトルを行列に全部くっつけたもの
\end{array}
\end{array}
\]
固有ベクトル(手作業)
| v_1 | v_2 | v_3 | v_4 | v_5 | v_6 | |
|---|---|---|---|---|---|---|
| c_1 | 0.4901 | 0.2711 | -0.2236 | -0.3268 | -0.6202 | -0.3801 |
| c_2 | 0.3312 | 0.2578 | -0.7554 | 0.1907 | 0.4037 | 0.2322 |
| c_3 | 0.4621 | 0.2175 | 0.4346 | 0.4718 | 0.3378 | -0.462 |
| c_4 | 0.4896 | 0.151 | 0.4194 | -0.2168 | -0.0234 | 0.717 |
| c_5 | -0.3322 | 0.6108 | 0.0379 | 0.5326 | -0.4267 | 0.2231 |
| c_6 | -0.2941 | 0.6456 | 0.115 | -0.551 | 0.3946 | -0.1563 |
検算
| v_1 | v_2 | v_3 | v_4 | v_5 | v_6 | |
|---|---|---|---|---|---|---|
| v_1 | -1e-04 | 0 | 0 | -1e-04 | -1e-04 | -1e-04 |
| v_2 | 0 | 0 | 0 | -1e-04 | 0 | 0 |
| v_3 | 0 | -1e-04 | -1e-04 | -1e-04 | -1e-04 | -1e-04 |
| v_4 | -1e-04 | 0 | -1e-04 | -1e-04 | -1e-04 | -1e-04 |
| v_5 | 0 | 1e-04 | -1e-04 | -1e-04 | 1e-04 | 0 |
| v_6 | 0 | 1e-04 | -1e-04 | -1e-04 | 0 | 1e-04 |
(ほぼ)0ばっかり! ですね。
完全に一致しないのは
計算手法や収束した、と判断するポイントなど
原因はさまざまです。
逆べき乗法
\[
x^k = A^{-1}x^{k-1}
\]
「逆」というだけあって逆行列を使ってます。
| v_6 | v_5 | v_4 | v_3 | v_2 | v_1 | |
|---|---|---|---|---|---|---|
| 手作業 | 0.02315 | 0.08504 | 0.1934 | 0.908 | 0.1934 | 1.517 |
| PRG | 0.02315 | 0.08504 | 0.1934 | 0.908 | 1.517 | 3.274 |
逆べき乗法では固有値、固有ベクトルを小さいほうから計算します。
ぱっと見、いい感じで計算ができているのですが
固有値が大きくなった時点で計算がおかしくなりました。
ある程度大きくなったらべき乗法に処理を変更するなど手段がいろいろあるようですが
あくまで紹介なので詳細が知りたいかたは是非調べてください。
ヤコビ法
\[
\begin{array}{l}
\Lambda = X^t A X \\
\begin{array}{l}
A &=& 対象の行列\\
\Lambda &=& 固有値*単位行列したもの\\
X &=& 固有ベクトルを行列に全部くっつけたもの
\end{array}
\end{array}
\]
固有ベクトル行列と元の行列をガチャガチャさせると固有値が計算できますよ
という方法です。
アルゴリズムにはみんな嫌いなサイン・コサイン・タンジェントが出てくるので
避けて通れるなら避けていきたい内容です。
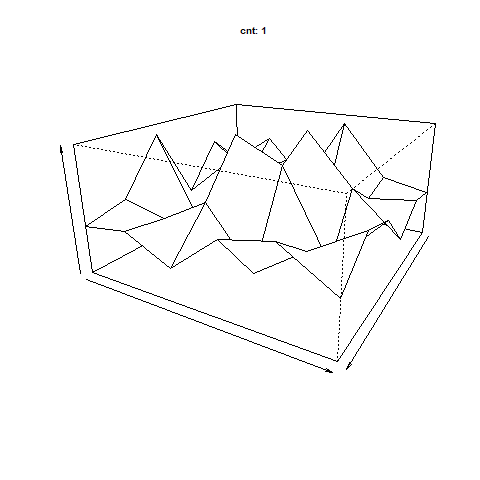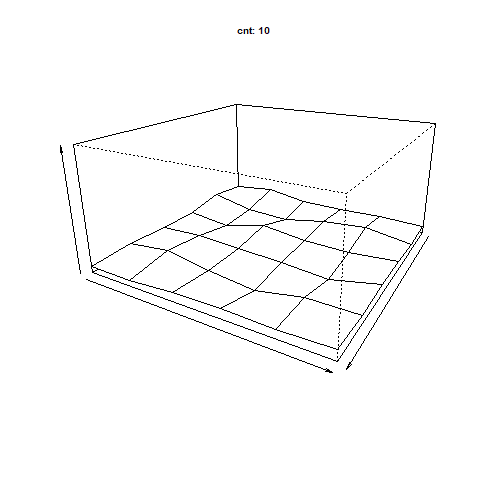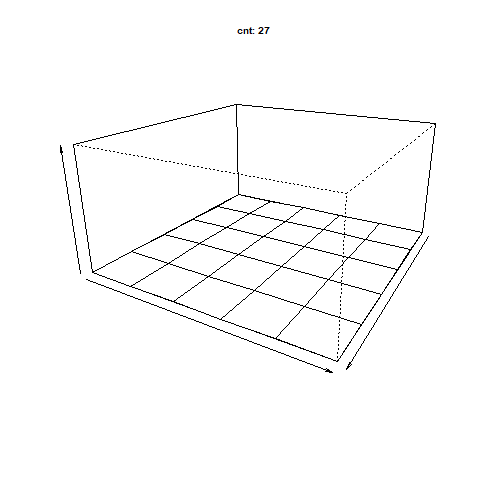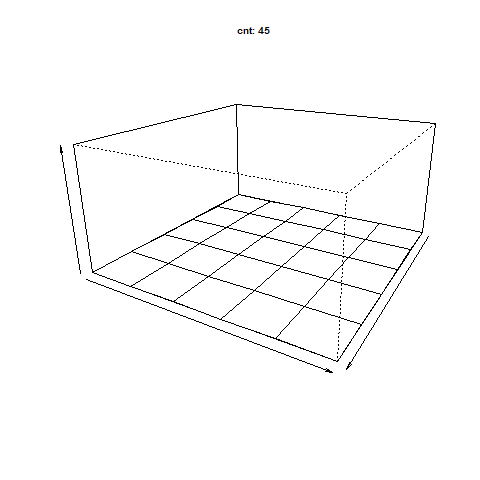
アニメーションは元の相関行列へ計算した結果を下記の数式を当てはめて比較したものです。
\[
A = X \Lambda X^{-1}
\]
ようは計算したベクトルと固有値で相関行列を再現すれば
元の相関行列との差分は限りなくゼロでしょう。というものを可視化したものです。
繰り返しの計算が進むごとに差分が小さくなっていくことが確認できます。
固有値計算の方法はたくさんある
少し前(2013年)のニュースで
スパコンの「京」が100行列の固有値計算を
いままで1週間かかったところ1時間でやった!
という記事がありました。
コンピュータの性能はもとより、より精度が高く、計算効率の良い固有値計算法を
プロの方たちは日夜いろいろ考えておられることでしょう。
ほかにもハウスホルダー法やQR法など、調べるとたくさんの手順が見つかりますので
興味があるかたは是非調べてみてください。
筆者はもうお腹いっぱいです。チス。