平均について_相加平均(算術平均)|Excel(エクセル)で学ぶデータ分析ブログ
■平均とは?
Wikipedia より
平均値とは、観測されるデータから、算術的に計算して得られる、統計学的な指標値である。
平均値という値はデータ分析の手続きにおいて最も使う機会の多い手法のひとつです。
テストの平均、年齢における体重の平均、所属する会社の平均年齢、年収など・・・。
日常会話でも使うことが多いため、馴染みのある言葉といえます。
ただし、データ分析の視点に立った場合、平均という手法はさらに細かく分類されます。
平均の種類
・相加平均:データの合計(sum)をデータの個数(N)で割ったもの(算術平均)。
→使いみち:科目別クラス平均、平均年齢、平均体重など
・相乗平均:データの積を1/N乗(冪根を取る)したもの(幾何平均)
→使いみち:19xx年~20xx年の経済成長率(%)における「平均成長率」など
・調和平均:データの値をひっくり返して(逆数)さらに相加平均してひっくり返した(逆数)もの(!)
→使いみち:行きは時速XXkm、帰りは時速YYkmの場合の「平均速度」など
と、対象となるデータによって手法を変えることで実値、実測に使い情報を読み取ることができます。
他にも、加重平均、移動平均、ベクトルの平均など・・・、全国の平均マニアにはたまらない平均手法がたくさんあります。
※この記事では相加平均にスポットを当てて説明をします(他手法は別記事にて)。
■相加平均(算術平均)について
下記表のようなデータには相加平均を使用することが一般的です。
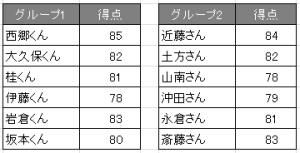
※使用されたデータに意図はありません。
一見した限りではどちらのグループの方が成績が良いかわかりづらい状態です。
こういった場合には下記のように
・各グループの合計点を取る
・各グループの平均点を取る
などをすることでグループ間の比較が可能となります。
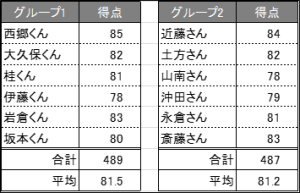
非常に僅差ではありますが、グループ1のほうが高いようです。
上記のように平均にはグループ間の比較をするための「指標」を作ることができるという特性があるため、分析手続きの中ではとても使う機会の多い手法となります。
■エクセルでの導きかた
エクセルの関数では
合計=sum
平均=averageを使用します。
関数【=SUM(B2:B7)】
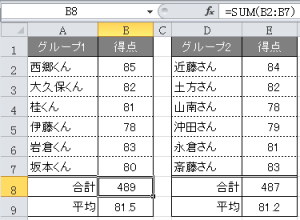
関数【=AVERAGE(B2:B7)】
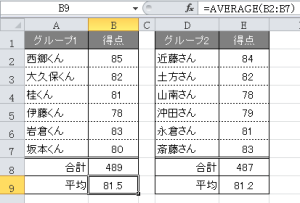
あるいは、データの個数が6個なので「合計値(489点)/データの個数(6人)=81.5点」という計算でも同じ結果となります。
関数【=SUM(B2:B7)/6】
■平均値の落とし穴
先ほどの結果、グループ1が僅差ではありますが比較するとグループ2に比べ高い平均値となりました。

「平均値が高い=全員が頑張った」と判断するには実はまだまだ情報不足です。
それを示す下記のデータを御覧ください。
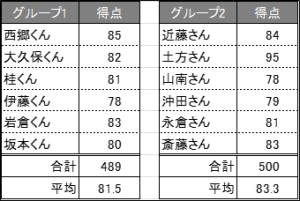
「アッーー! グループ2の平均値が2点も高くなっているよ!」
一見するとデータに違いはありませんが、よぉぉく見ると
「土方さんの点数が上がっている!」
ということで、何をお伝えしたいのかといいますと、
・データの個数が少ない
・ひとつのデータが極端に高い数値
などになった場合に、平均値は大きく変動してしまうという点です。
したがって、平均値でデータを評価する場合には
・分散や標準偏差を見る。
・5数要約値(中央値、四分位点、最大値、最小値、最頻値)を見る
などをおこなって、極端に高かったり低い数値(はずれ値)などを確認することが重要です。
■追伸
余談ですが、統計の手続き上では平均を「mean」と呼称するのが一般的です。
日常では平均を「average(アベレージ)」という言葉で使う機会が多いのでmeanは聞き慣れないように思います。
厳密には先に述べました「相加平均=mean」となり、「中央値(median)、最頻値(mode)なども含めた広義の平均=average」という使い分けがされるようですが、
ではなぜエクセルの相加平均の関数はaverageなのだ? という疑問も浮かんだり。
統計の世界は奥が深いですね。



