分散について|Excel(エクセル)で学ぶデータ分析ブログ
■分散とは?
Wikipedia より(一部編集)
分散(variance)は、確率論において、確率変数の分布が期待値からどれだけ散らばっているかを示す値。
平均値の記事でも書いておりますが、平均値は他群の比較において重要な指標となりますが、極端に高かったり低い数値が含まれていた場合には大きく平均値に影響を与えることがあり、平均値だけで全てを評価することは難しいという欠点がありました。
そんな平均値を別の視点から評価する際に重要な指標となるのがこの分散となります。
■分散の使い方
平均と同様のデータを使用します。
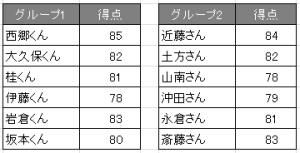
※使用されたデータに意図はありません。
今回は合計、平均だけでなく、分散の値も表示します。
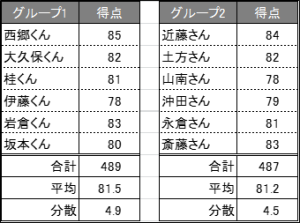
分散の読み方は、「値が小さいほど『バラつき』が少ない」と読み取って下さい。
つまり、グループ1は平均値81.5で、4.9のバラつきがあり、グループ2は平均値81.2で、4.5のバラつきがあります。
したがって、平均値はグループ1が高いが、バラつきはグループ2の方が低いといえます。
低いからなんだ、と言いたくなるのをグッとこらえてください。誰しも抱く疑問でございます。
データ分析にとって、バラつきがあったりなかったりすることは非常に重要です。
なぜなら、仮にグループ1と2にそれぞれ指導者(先生)がいたとして、同じテストの結果、生徒がバラつきが少なくテストの結果を出した場合には、これは評価できることだと思いませんか?
平均の記事でも説明したとおり、少数の標本数においては1人の結果が大きく平均値を変える力を持っています。しかしその場合、特定の生徒がいるお陰でクラスの平均点が上がっている→クラス全員が賢いという誤った判断(誤読)のおそれが発生します。
その際、同時に分散の値も見ることで、等しくみんながテストを頑張っているのか、一部の生徒が底上げをしているのかを判断するためには、非常に重要な指標といえます。
したがって、敢えてグループ1と2の評価をするとすれば、
「グループ1が平均値では上回っているが、それは西郷くんの頑張りのお陰である」
という読み方もできるのです。
■エクセルでの導きかた
エクセルの関数では、
分散=var.p(他にvar, var.s, varpなどあるので別の機会に説明)を使用します。
関数【=VAR.P(B2:B7)】
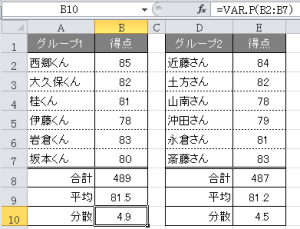
力技で出力する場合には下記の手続きをしてください。
(グループ1を例に計算)
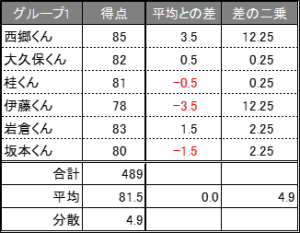
ご自身で手計算していただくとわかりますが、
西郷くんの得点-平均値、大久保くんの得点-平均値…といったように6名分差を出力したあとにその値の平均値を出すと必ず「0」になります。
でも、その「平均との差」に対して二乗をした上で平均値を出すと、それは分散の値となるのです。
つまり、分散という値の導出は
「(個別の値-平均値)の二乗を平均した値」といえます。
■土方さんのがんばりはどんな結果をもたらすのか
平均の計算で使った土方さんがとてもがんばったデータを使った場合、どのような分散の値になるでしょうか。
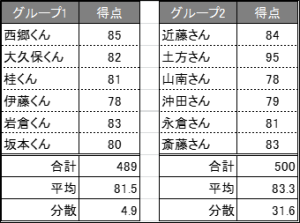
いうまでもなく、ものすごい勢いでバラついてますね。
これでは平均値の底上げは達成できたとしても、グループ1の方が全体的には頑張っていると言いたくなってしまいます。
以上のように、分散の値はデータのバラつきを把握するためには重要な指標といえます。
然しながら、分散の値が「何を意味しているか」に関してはちょっと表現がしづらいのです。
それは「差を二乗する」という手続きが大きく影響しており、二乗した結果、実値とはかけ離れた値となってしまい、イメージがつきずらくなっているのが実情です。
この「わけのわからない値」を「なんとなく理解できる値」にするために、標準偏差という値がありますが、それはまた別の機会に紹介させていただきます。