標準偏差について|Excel(エクセル)で学ぶデータ分析ブログ
■標準偏差とは?
Wikipedia より(一部編集)
標準偏差(Standard Deviation)は、分散の正の平方根である。統計値や確率変数の散らばり具合(ばらつき)を表す数値のひとつ。
分散の記事において、値が「何を意味しているか」に関してはちょっと表現がしづらいと説明をしました。
理由は個別データの「差を二乗した平均」という計算手続きを経て得た値のため、その値を見ただけで何を示しているのか分からないという点です。
ではその値の平方根ならいいじゃないか、と言われれば、その通りです。
平方根であればなんとなく理解できる値になります。
■標準偏差の使い方
平均や分散と同様のデータを使用します。
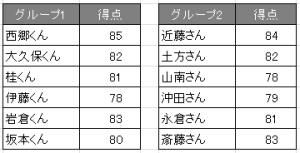
※使用されたデータに意図はありません。
今回は合計、平均、分散だけでなく、標準偏差の値も表示します。
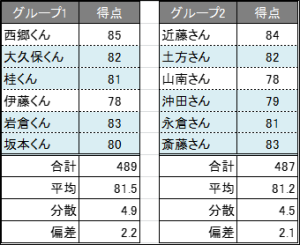
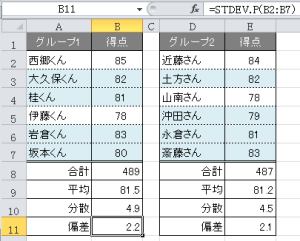
読み方は「グループ1のデータのほとんどは、平均値81.5点の前後(±)2.2点の間にほとんどのデータが含まれており、グループ2のデータのほとんどは、平均値81.2点の前後(±)2.1点の間にほとんどのデータが含まれている」といったように読み取っていきます。
ざっくりと確認してみると、上表の青色のデータはそれぞれ先に述べた値の範囲に含まれていることが確認できます。
比率でいうと4/6=2/3=0.6666=66.6%といったところでしょうか。
この「ほとんど」という表現が絶妙でして、これはめくるめく統計迷宮への入り口になる重要な表現だと個人的には考えておりますが、この記事でこの「ほとんど」を厳密に伝えていこうとなりますと、途端に文章が長くなっていきますのでまた別記事にて説明させていただきます。
■エクセルでの導きかた
エクセルの関数では
分散=stdev.p(他にstdev, stdev.s, stdevpなどあるので別の機会に説明)を使用します。
関数【=STDEV.P(B2:B7)】
力技で出力する場合には下記の手続きをしてください。
グループ1を例に計算しております。
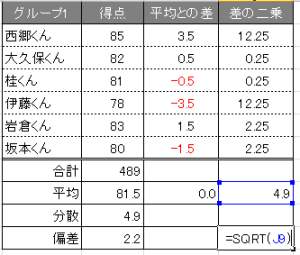
SQRTという値の平方根を計算する関数を使うと、同じ結果になります。
■偏差と分散の関係
「分散の平方根=標準偏差」であり、「標準偏差の二乗=分散」であるわけですが、これが数式によって標準偏差で表現したり、分散で表現したりと導出の際には混乱することも多い存在です。
例えば正規分布の数式には標準偏差の値を組み込みますし、相関係数の数式には分散を使用します。
個人的には計算過程では分散で、分析過程では標準偏差を使った方が理解が早いと考えておりますが、それはもう人それぞれ好みが「バラつく」ということで、またの機会にご説明させていただきます。
ところで、学歴社会の昨今では「偏差値」なる指標が社会の根幹を成すほどに領有権を得ておりますが、この偏差値も標準偏差の値を加工したものです。この記事では冗長が過ぎるので、また別の機会にご紹介させていただきます。