単回答・複数回答で読み間違いのない集計・グラフの作り方|Excel(エクセル)で学ぶデータ分析ブログ
※ざっくり読み解く 多変量解析始めました。
■単回答・複数回答で読み間違いのない集計・グラフの作り方
アンケートなどの調査報告書では円グラフと棒グラフが大活躍します。
●円グラフ
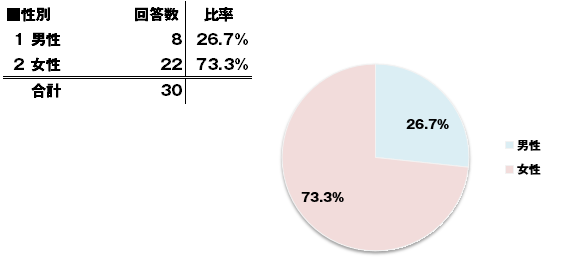
●棒グラフ
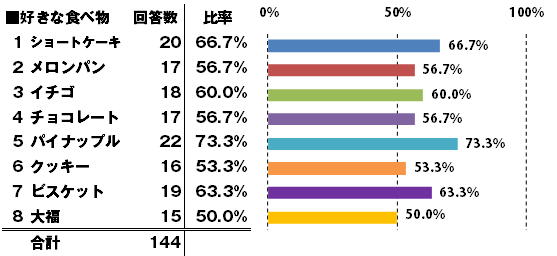
ただ、弊社で「昨年度を参考に」とお預かりした際、3回に1回くらいは「集計の仕方の誤り」を見つけることがあります。
調査報告書の計算の仕方を誤ると、読み違いを起こすおそれのある内容を紹介しようと思います。
■単回答と複数回答
●単回答について
例えば性別や年齢は「1回答者あたり1項目」しか選択できない設問になります。
あたり前ですが、「私の年齢は20歳と30歳です」とは答えませんね。
●複数回答について
しかし、「好きなものはなんですか?」と聞かれたら、なかなか「イチゴです。それ以外は嫌いです」とは答えづらいと思います。キリンさんが好きと答えれば、でもゾウさんのほうがもっと好きですと答えたくなるのが人というものですね。
そんな時にはいくつでも選択できる複数回答を使いましょう。
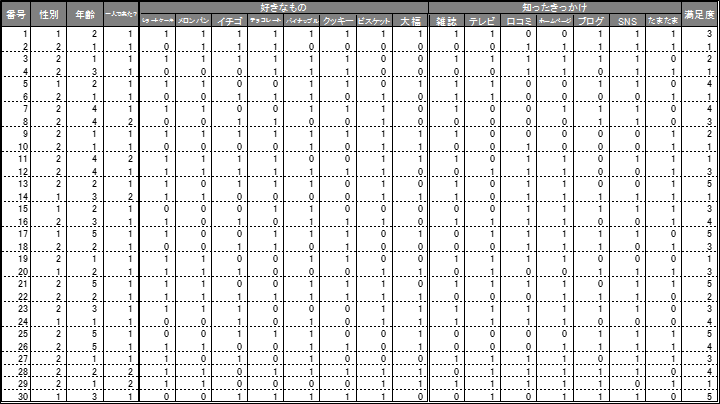
■複数回答の集計方法
下記の2つの表を見比べた際に、「あれ、何か違う?」とすぐ気づいたあなたは、めくるめく分析の迷宮に入り込んでいることでしょう。原因が分かる方はもうこの記事読まなくてもいいかもしれません。
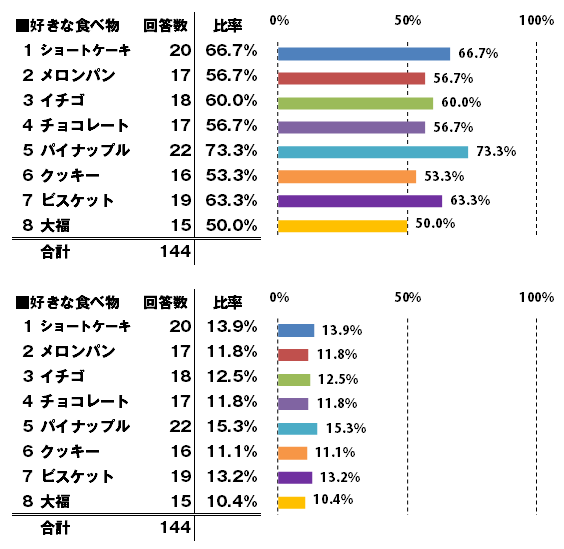
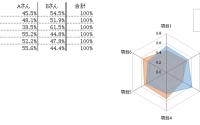
上の集計グラフと下の集計グラフでは、集計の値は同じですが比率もグラフのサイズも異なります。
同じ集計データでこういった現象、まず単回答ではおきません。
■回答数で割る? 回答者数で割る?
前述した「誤った集計」は、ずばり下の集計グラフです。下の集計グラフはそれぞれの回答を「合計回答数」で割っています。ゆえに「20/140=13.9%」という計算結果となりますが、これって何か意味があるのでしょうか?
このデータの合計回答数は「30名」です。30名のうちショートケーキを好きと答えた方が「20名」いれば、「20/30=66.6%」となるのが自然ではないでしょうか。30名がそれぞれ3~4種類の好きな食べもを選択した結果、、回答数が144回答あっても、その数字にはたくさんの重複が発生していることを忘れてはなりません。
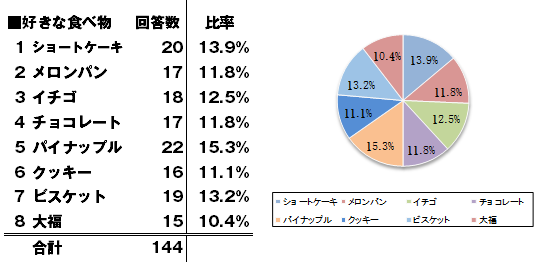
さらに円グラフなんかで出してしまうと、もう原型がなくなってしまいます。これでは
ショートケーキを好きと答えた人は30名×13.9%=およそ3~4人程度か、という誤読を起こしてしまいます。
「複数回答の円グラフはダメ!! ゼッタイ!!」
■数字のごまかしかた。
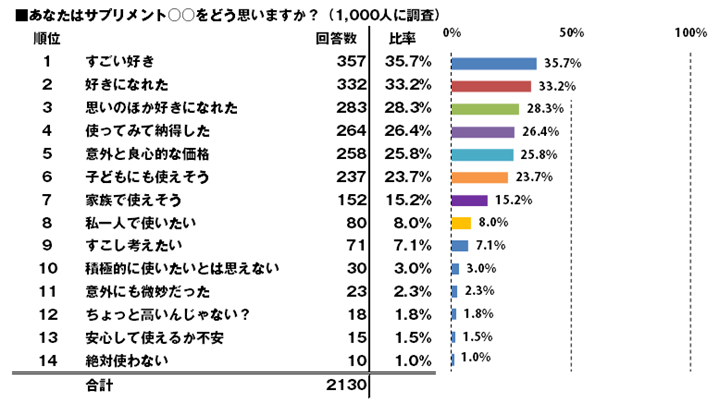
たまにこういったデータを深夜の通販とか昼前の地方局で見ることがあります。
ここまではなるほど、という感じなのですが、ときどきこんなキャッチが入ります。
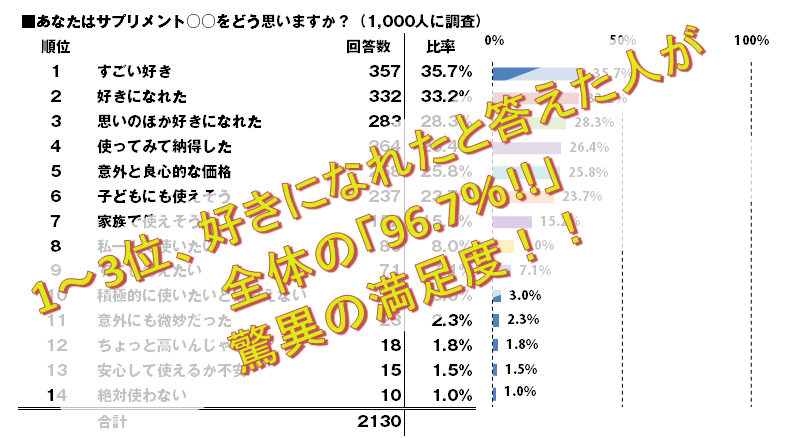
ズッコケそうになりますが、意外とみんな「へぇ~すごいなぁ」と言ってしまうから驚きです。こういったところから学ぶものは多いですね。