カイ二乗分布について|Excel(エクセル)で学ぶデータ分析ブログ
■カイ二乗分布とは?
Wikipedia より(一部編集)
“カイ二乗分布(Chi-squared distribution)、またはχ2分布は確率分布の一種で、推計統計学で最も広く利用されるものである。”
検定に関してはあらためてまた説明の記事を作ろうと思いますが
検定手法にカイ二乗検定という手法があります。
このカイ二乗検定にて使用する確率分布こそカイ二乗分布です。
とても面白い仕掛けになっておりますのでご紹介したいと思います。
■カイ二乗分布の概要(まずは二項分布と正規分布の説明)
トランプカードを例にします。
引いたカードが赤ならば1点、黒ならば0点という採点方式で10回やり採点。それを10ゲーム行います (カードは引くごとに戻します)。
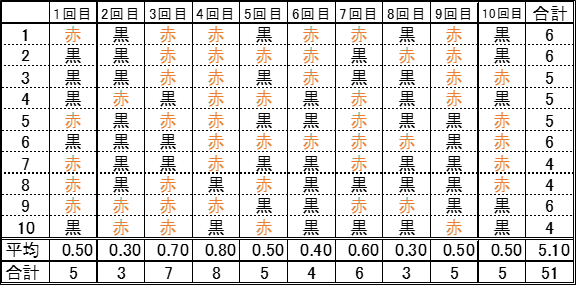
確率1/2で赤が出るため、それぞれのゲームの合計得点は5点に近づくことがなんとなく想像できます。また、10ゲーム行った結果の平均は5.1点で、合計点の平均である5点と近似しています。
全体の傾向をつかむためにデータを大きくしましょう。
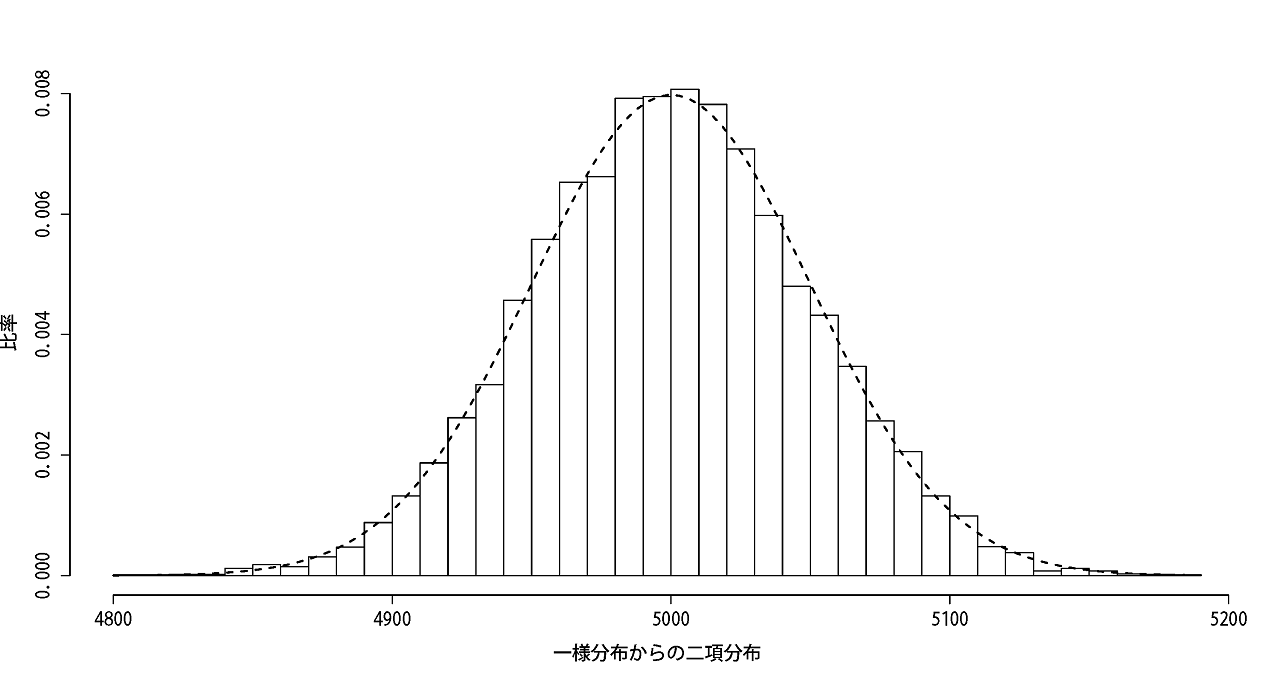
先ほどの試行を10,000回カードを引き、それを10,000ゲーム行いました。おかげで十分なくらいデータがバラついていますね。
これは二項分布B(n=10,000, p=0.5)に従います。加えて、正規分布N(μ=5,000, σ=50)にも近似しています。
破線は二項分布で描いても正規分布で描いても同じ線を得ることができました。
ここまでは一様分布、二項分布、正規分布のお話です。この記事はカイ二乗分布に関する記述でしたので、これからが本題です。
■カイ二乗分布の概要(カイ二乗分布の説明)
正規分布のデータは平均を中心に左右にバラつきますが、あるゲームの結果(合計点)と平均までの「距離」を考えます。
距離は (データ-平均)で計算ができます。
でも、これでは±の符号がつきますので二乗して符号を消します。(データ-平均)^2
更に尺度を標準化するために平均で割ってみましょう。{(データ-平均)^2}/平均
赤が5, 010点の場合の誤差={(5, 010-5,000)^2}/5,000=0.02
対して赤が5, 010点ならば黒は4,990回出たことがわかりますが、
これも{(4, 990-5,000)^2}/5,000=0.02となるので合計して0.04を誤差(距離)の指標とします。
こういった値を積み重ねて度数分布表を作成すると下図の右側の結果を得ました。
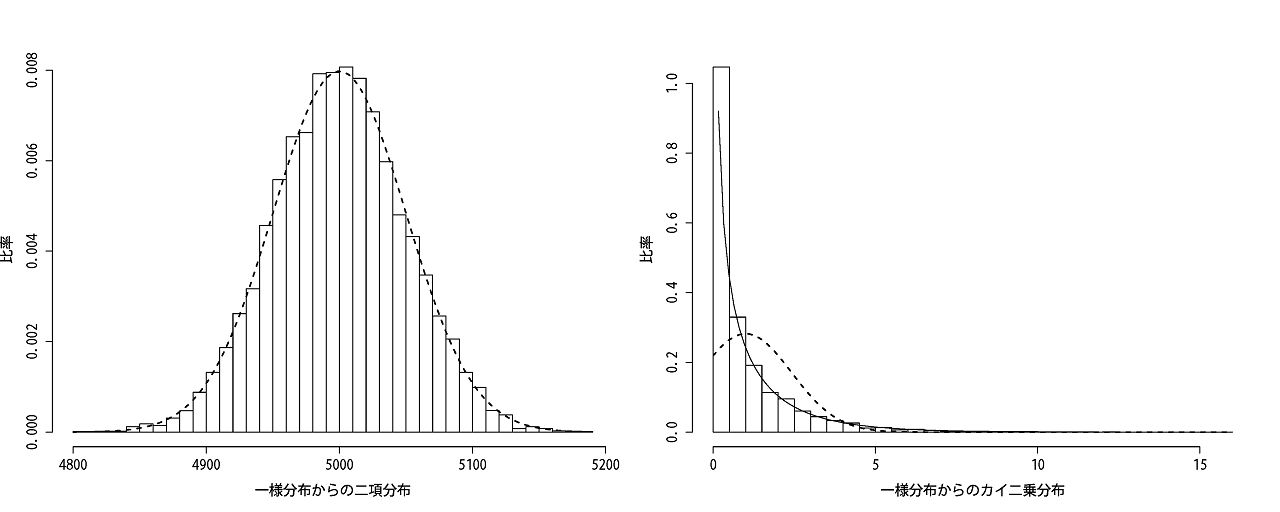
この値こそカイ二乗分布と呼ばれる分布です(実線)。
カイ二乗分布の特徴は「自由度と呼ばれる一つの情報だけで描くことができる」点にあります。
例えばカードの試行は「赤:黒=1:1」の確率1/2という条件下で行いましたが
これが「スペード:それ以外=1:3」でも「10以下の数字:絵札=40:12」という条件でも同じ分布を得ることができます。
試しに「10以下の数字:絵札=40:12」の条件を採用して計算してみましょう。
(10,000回カードを引き、それを10,000ゲーム行います)
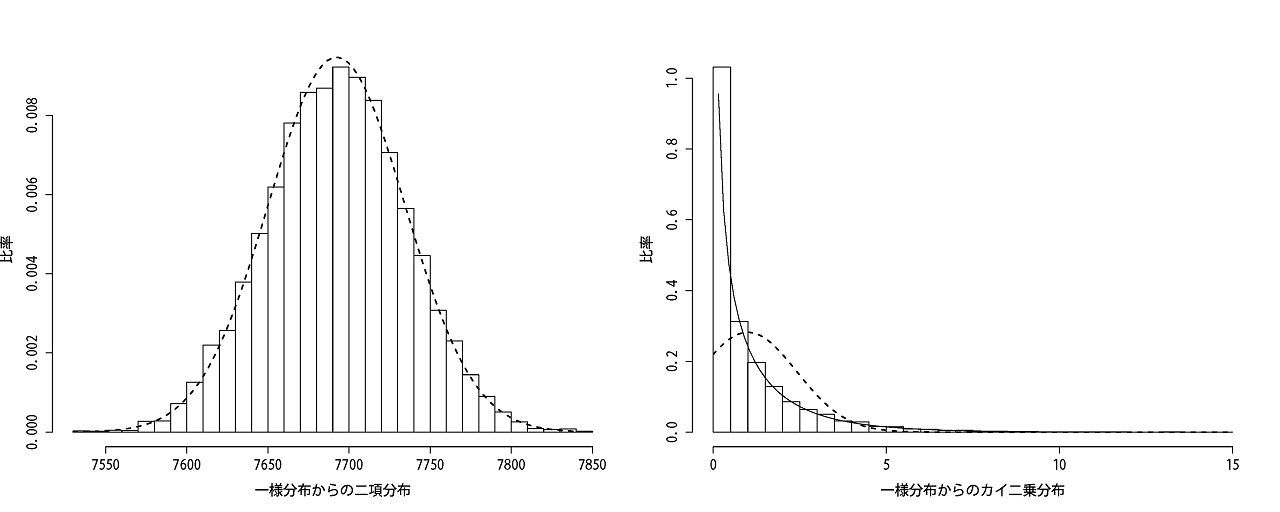
グラフだけで説得力がありませんが、絵札以外なら1点ということで確率は40/52≒0.76となり、平均≒7,692を中心にばらつくはずです。
対して絵札の平均は10,000-7692≒2,307で、それを中心にデータがバラつきます。
あとは誤差の指標をそれぞれ計算し合計すると先ほどと同じような分布の結果(右)となりました。
ちなみに、現在図示している分布は「自由度1のカイ二乗分布」と呼び、自由度という言葉が出てきます。
この自由度という値はやんわりと理解するには簡単ですが、理論的に理解するにはとても大変です。
カードの赤×黒や絵札×10以下など2つの情報があるから「2-1=自由度1」ぐらいに考えて下さい。
■自由度5のカイ二乗分布
サイコロの出目は6ですから自由度は「6-1=5」となり自由度5のカイ二乗分布を得ることができます。
(10,000回サイコロを振り、それを10,000ゲーム行います)
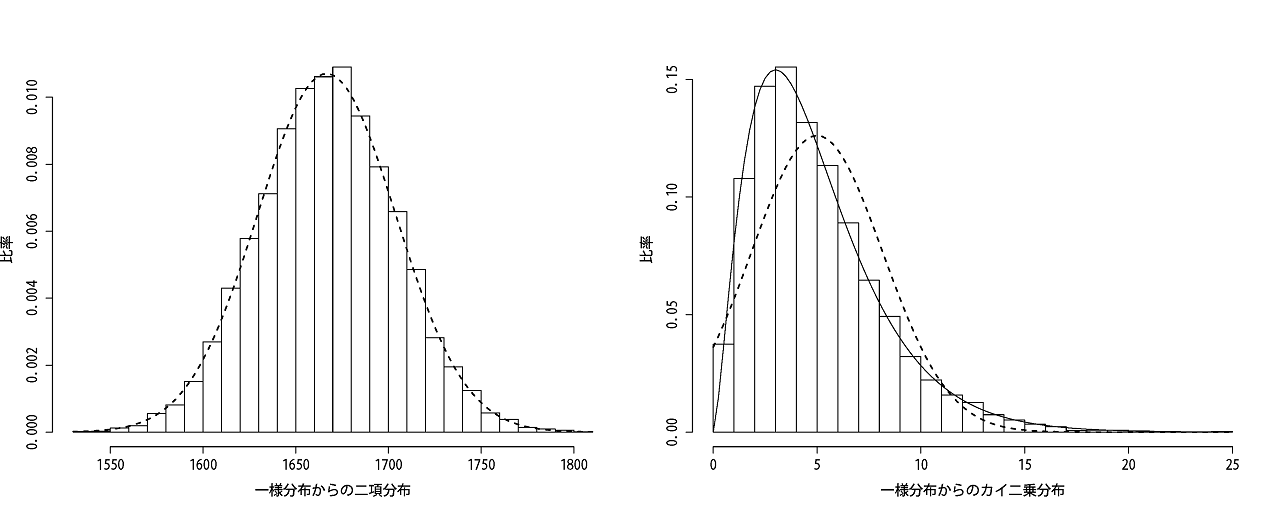
確率は1/6=0.1666ですので平均≒1,666を中心にバラつきます。
今度は自由度が5になったので今までと分布が異なります。ちょっとだけ山型の曲線になってきました。
■自由度が増えると正規分布に近似します
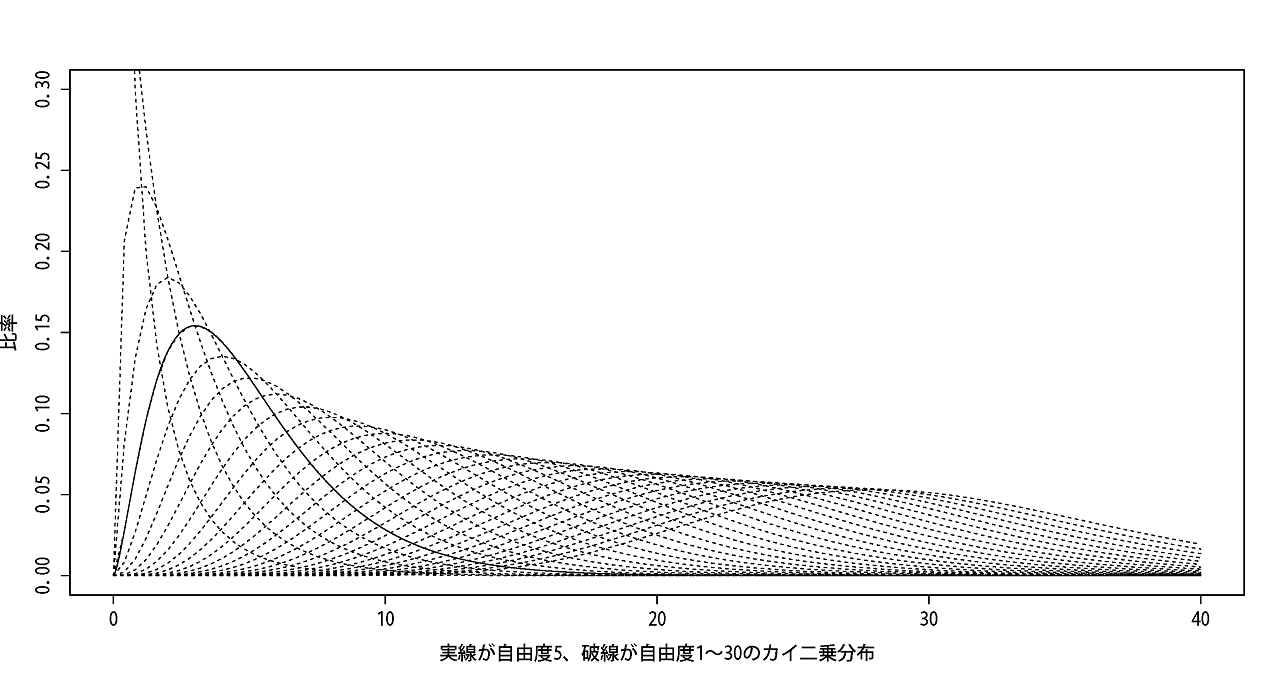
上図は自由度1~30までのカイ二乗分布です。自由度が増すごとに曲線がキレイな山型になっていきます。
もしかしたら自由度が増加すると正規分布みたいにキレイな曲線を描くかもしれません。
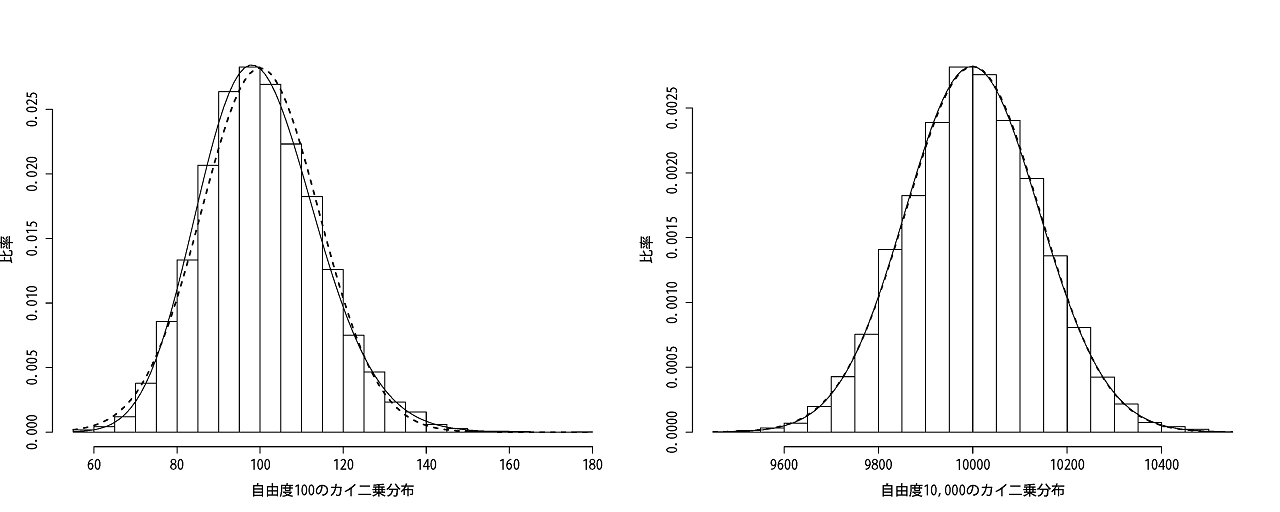
その通りです。実線がカイ二乗分布で破線が正規分布の曲線です。自由度の値が低いときには左に分布が寄っていましたが
自由度が高くなると左右対称に近づくことで正規分布と似た形になっていきます。
いろいろとグラフだけで説明をしていましたが、カイ二乗分布に従う条件は下記です。
変数 X_1・X_2・X_3・・・X_kがそれぞれ標準正規分布(平均=0、標準偏差=1)に従うとき
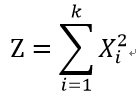
で得られた値(統計量)はカイ二乗分布に従います。
関数で書くと
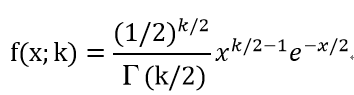
k=自由度です。もう数字を書いているのか記号を書いているのかわかりません。
Γという文字は「逆さL」と呼びます。嘘です。ガンマと呼びます。
このガンマという記号がなぜ突然やってきたのかというと、ガンマ関数という特殊な関数を使って計算するからですが、
これはまた別の機会に紹介します。
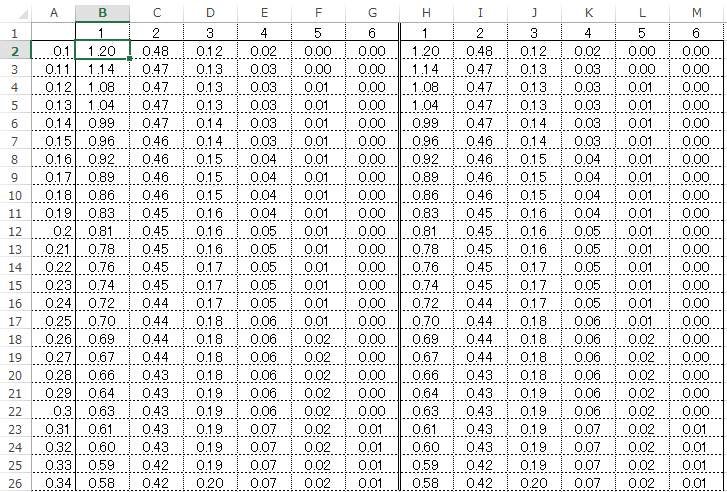
エクセルでは下記のようにかきます。
【(((1/2)^(B$1/2))/GAMMA(B$1/2))*$A2^((B$1/2)-1)*EXP(-$A2/2)】
または元々あるカイ二乗分布の関数を使い
【CHISQ.DIST($A2,H$1,0)】と書くほうが無難かもしれません。
■あらためてカイ二乗分布の特徴
カイ二乗分布は確率分布を利用した分析手法の中ではとてもよく使われます。
自由度という1つの情報(パラメータ)で確率を計算できるため一見簡単なように見えますが、
仕組みを理解しようとするとけっこう大変だったりします。
また、カイ二乗分布をベースにF分布やt分布も生成できるのですが、それはまた別の記事にて。