二項検定について【実践編】|Excel(エクセル)で学ぶデータ分析ブログ
この記事では二項検定について実事例を元に紹介しています。
※二項検定の基本的な考え方は下記の記事をご覧ください。
→基本編へ
例題「イカサマ賭博師との闘い」
よしおくんが池袋のとある路地裏で、いかにも賭博師なおじさんに話しかけられました。
「サイコロで勝負をしよう。1~5が出たら君に1点あげよう。
その代わりに6が出たら私に3点をくれないか?
60回振った合計得点が高い方に、低いほうが10,000円支払うんだ。やるかい?」
よしおくんは頭のなかにパソコンが埋め込まれているので下記のとおり計算しました。
まず、サイコロの各出目の出現率は一様分布にしたがうから5/6の確率で僕に1点が入るな。
賭博師には1/6の確率で3点が入るわけだから
60回後には期待値として
僕:\(60 \times (5/6) \times 1 = 50点\)
賭:\(60 \times (1/6) \times 3 = 30点\)
入るはずだ。
| 1~5が出たら | 6がこれだけ出る | よしおの得点 | 賭博師の得点 | 差 |
|---|---|---|---|---|
| 40 | 20 | 40 | 60 | -20 |
| 41 | 19 | 41 | 57 | -16 |
| 42 | 18 | 42 | 54 | -12 |
| 43 | 17 | 43 | 51 | -8 |
| 44 | 16 | 44 | 48 | -4 |
| 45 | 15 | 45 | 45 | 0 |
| 46 | 14 | 46 | 42 | 4 |
| 47 | 13 | 47 | 39 | 8 |
| 48 | 12 | 48 | 36 | 12 |
| 49 | 11 | 49 | 33 | 16 |
| 50 | 10 | 50 | 30 | 20 |
| 51 | 9 | 51 | 27 | 24 |
| 52 | 8 | 52 | 24 | 28 |
| 53 | 7 | 53 | 21 | 32 |
| 54 | 6 | 54 | 18 | 36 |
| 55 | 5 | 55 | 15 | 40 |
6が15回でドロー。もし16回以上出たら負けてしまう。
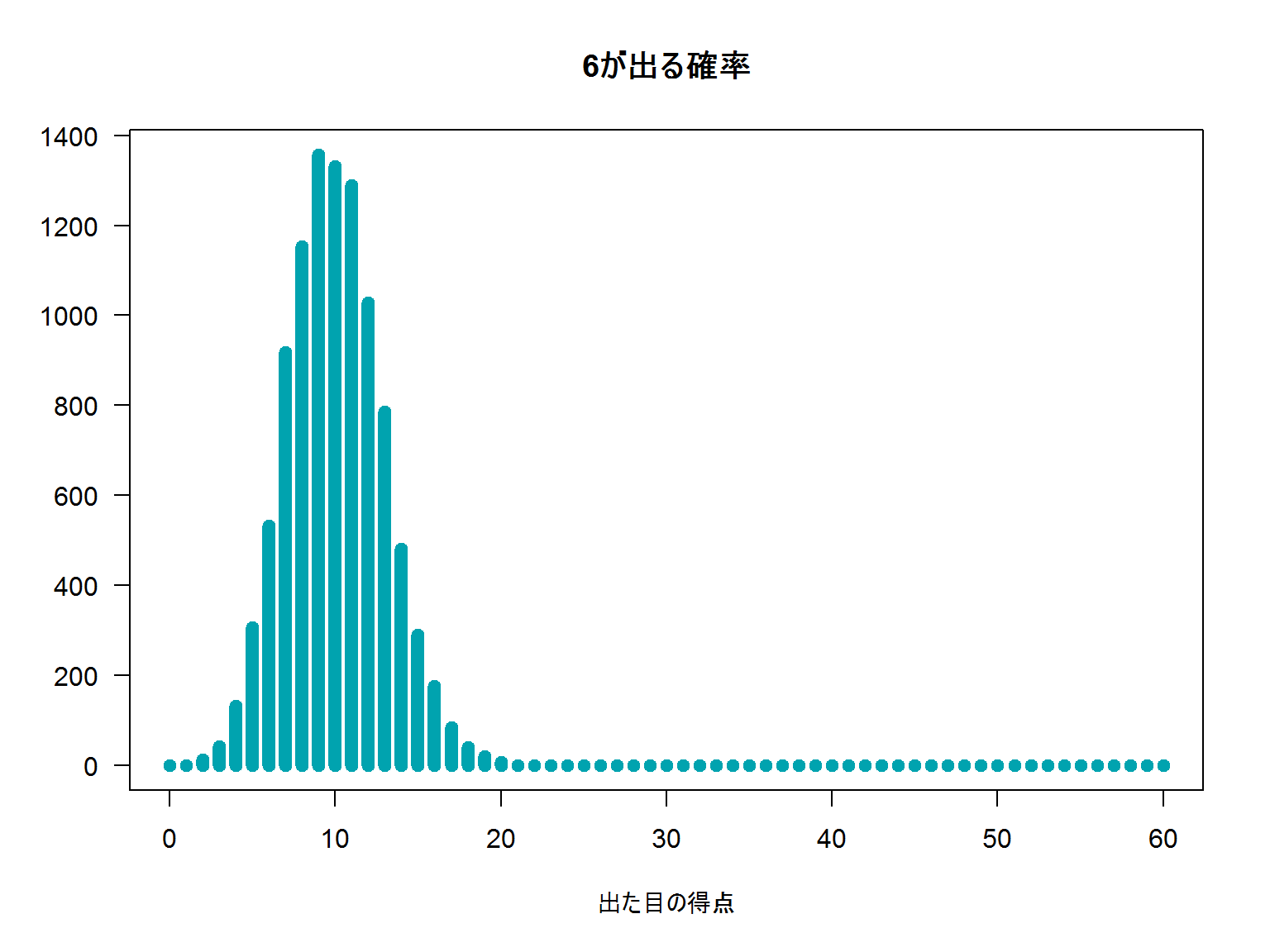
でも、6が16回以上出る確率なんて
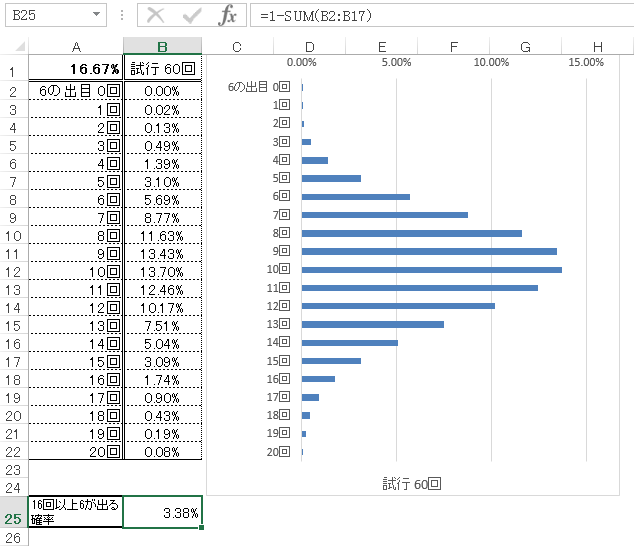
ほとんどないじゃないか。
これは、勝てる!
「1,000回やりましょう。」
結果
| よしおの得点 | 賭博師の得点 | 勝敗 |
|---|---|---|
| 43 | 51 | Lose |
| 41 | 57 | Lose |
| 38 | 66 | Lose |
| 35 | 75 | Lose |
| 39 | 63 | Lose |
| 46 | 42 | Win |
| 39 | 63 | Lose |
| 46 | 42 | Win |
| 46 | 42 | Win |
| 41 | 57 | Lose |
結果はごらんの通り。惨憺たるものでした。
「それでは負けた分の銭払ってもらおうかい!!」
| 勝敗 | |
|---|---|
| 勝ち | 220 |
| 負け | 685 |
| 引き分け | 95 |
| 負けた差額 | 465 |
∴4,650,000円の支払いが発生した!!ということで、哀れよしおくんはしこたま現金を奪られましたとさ。
…となるわけもないのがよしおくんのクレバーなところです。
いままで計算した過程を理路整然と説明し、イカサマ賭博師がぐぅの根もでないほど徹底的に論破しました。
「期待値10×3=30点の中でこのような得点を得られることは サイコロの確率からして有意に『ありえない』と思うのだが どう思いますか、イカサマ賭博師さん」
賭博師は「覚えてやがれ!」と捨て台詞を吐いて退散しました。
二項検定のまとめ
検定のポイントは、まず「理論上起きうる現象」を設定することからはじまります。
今回であれば確率1/6で60回の二項分布にしたがう試行が「理論上起きうる現象」です。
「サイコロを60回投げたときに6が16回以上出たらサイコロの出目にかたよりがないか、『理論上起きうる現象』と比較しよう」
これを難しくいうと「帰無仮説」などと呼びます。
実際、イカサマ賭博師の使用したサイコロの出目は6が出やすいように微妙に重さをコントロールしたサイコロでした。
厳密には
5/7の確率で1~5が出て
2/7の確率で6が出るというサイコロです。
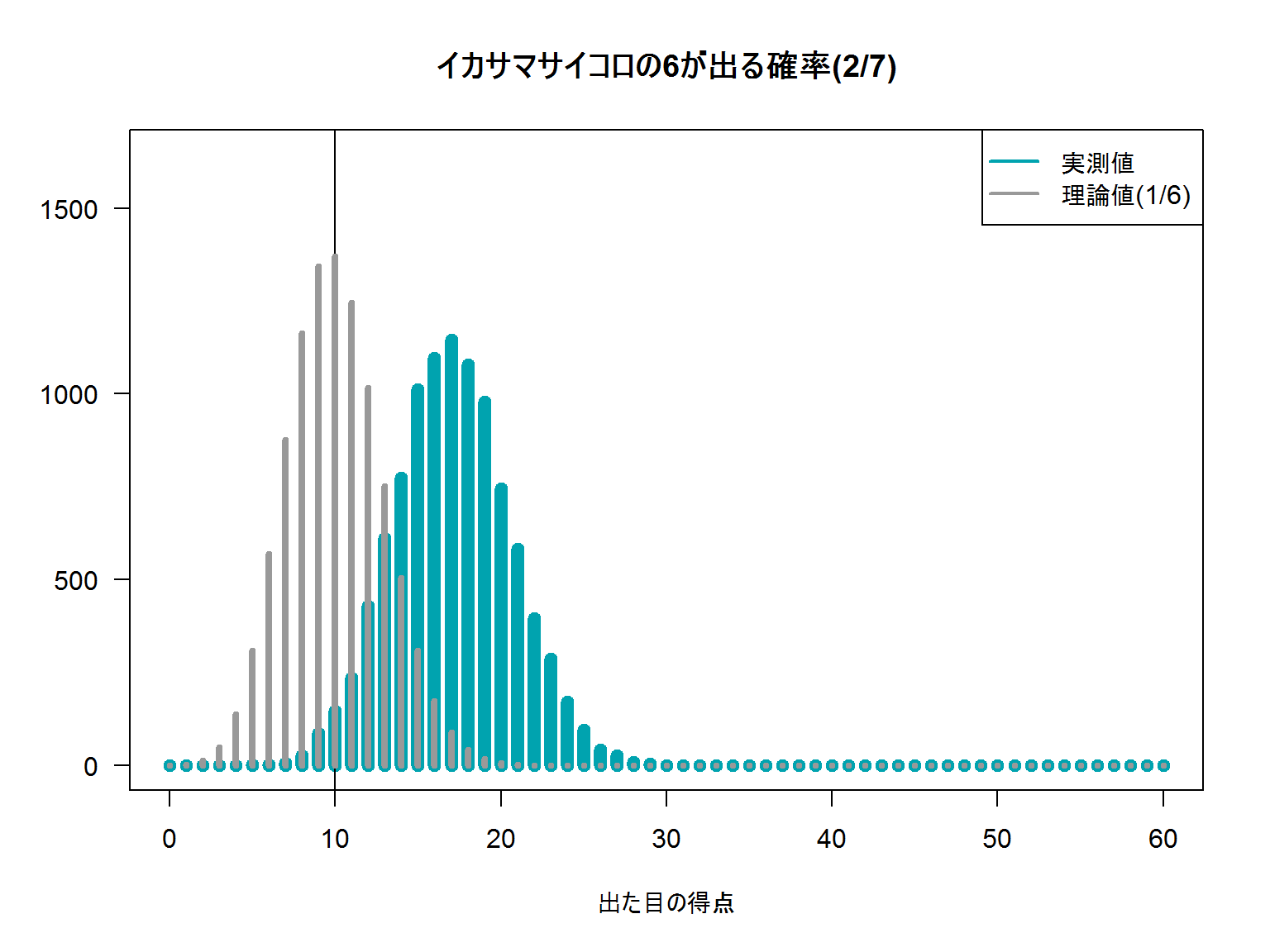
理論値の分布とくらべて明らかに出現頻度が異なります。
この理論値が「帰無仮説の確率分布」です。よしおくんが最初に考えたモデルですね。
で、これが結果的には青い分布になりました。
平均がおおよそ17のあたりになっていますが、平均17回×3点=51点も取られては勝てるわけがありません。
本来、「確率1/6で60回の二項分布にしたがう試行」において17回以上6が出る確率は1.64%程度のはずです。
にも関わらずトータルで負けた=その出現率おかしくない? と言えるわけです。
また戦績を元に平均得点を割り出したもので二項検定を行いました。
よしおくんの平均得点:42.919賭博師の平均得点:51.243| 結果 | 試行回数 | P値 | 片側・両側検定 |
|---|---|---|---|
| 17 | 60 | 0.01645 * | 片側検定 |
先ほどの確率と同じ結果が出ました。
以上が二項検定の実践編となります。
次はもうちょっと現実的なデータを取り扱います。
→応用編へ