ざっくり読み解く 因子分析【多因子分析編】
はじめに
1因子数で因子分析をやってみる、で因子負荷量に九九っぽいものを入れると
九九表っぽい相関行列が得られたことを確認しました。
今回は複数の因子を用いて、いくつか極端な場合を確認してみます。
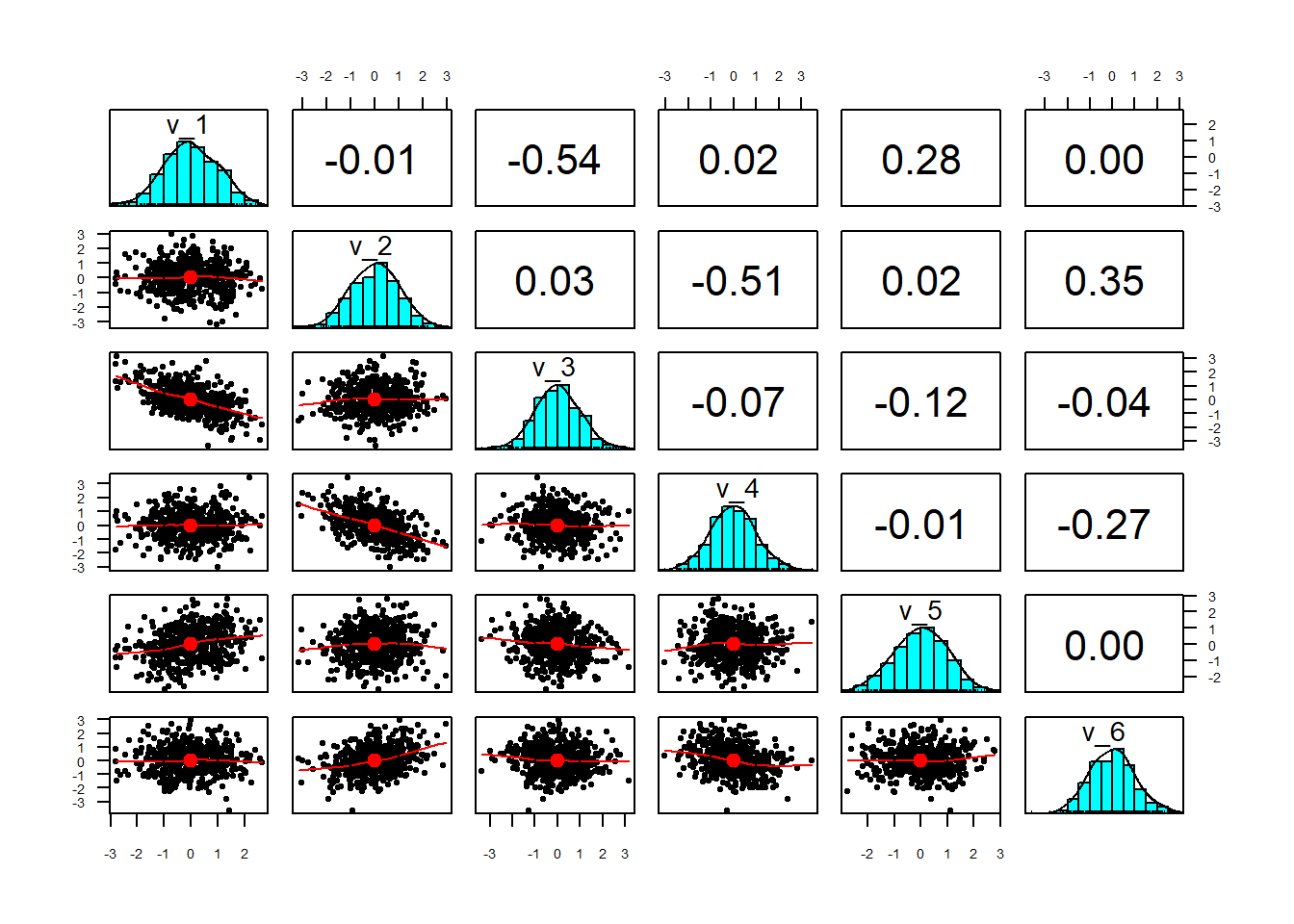
2因子の場合
| fc_1 | fc_2 | |
|---|---|---|
| v_1 | 0.9 | 0 |
| v_2 | 0 | -0.9 |
| v_3 | -0.5 | 0 |
| v_4 | 0 | 0.5 |
| v_5 | 0.3 | 0 |
| v_6 | 0 | -0.3 |
理系文系みたいな区分を極端に分割したようなイメージです。
また、符号をそのままにすると面白みに欠けるので、符号も一部入れ替えました。
| fc_1 | fc_2 | Factor1 | Factor2 | |
|---|---|---|---|---|
| v_1 | 0.9 | 0 | 0.997 | -0.026 |
| v_2 | 0 | -0.9 | 0.011 | 0.813 |
| v_3 | -0.5 | 0 | -0.545 | 0.043 |
| v_4 | 0 | 0.5 | 0.004 | -0.626 |
| v_5 | 0.3 | 0 | 0.278 | 0.022 |
| v_6 | 0 | -0.3 | 0.015 | 0.432 |
左(fc_1/fc_2)が計算前の因子負荷量のベースになったもの
右(Factor1/Factor2)がその情報をもとにランダムデータを作成したものを2因子数で因子分析した結果です。
順序や符号が変わったりと一見すると合わないように見えます。
これは説明が長いので省略、言いたいところですが
Rの因子分析関数はソートローディングという内部関数が組み込まれており
分析上、都合が良いようにちょっとコントロールされてるんだなーくらいに思っておいてください。
つまり、ざっくりいうと計算ソフトや関数によって結果が微妙に変わります、ということです。
過去記事からしつこく書いている、「ややこしい」の一端が垣間見えます。
このあたりを詳しく知りたいかたは、もう「因子分析 詳しく」などで調べるほかありません。
なんか絵がほしいと思ったので因子負荷量のベースになったもの(黒)と因子負荷量(赤)をプロットしました。
確かに向きが変わっているように思いますが、逆にいうと、向きくらいしか変化が起きてない、ということで
計算元になった情報を保っていることが確認できました。
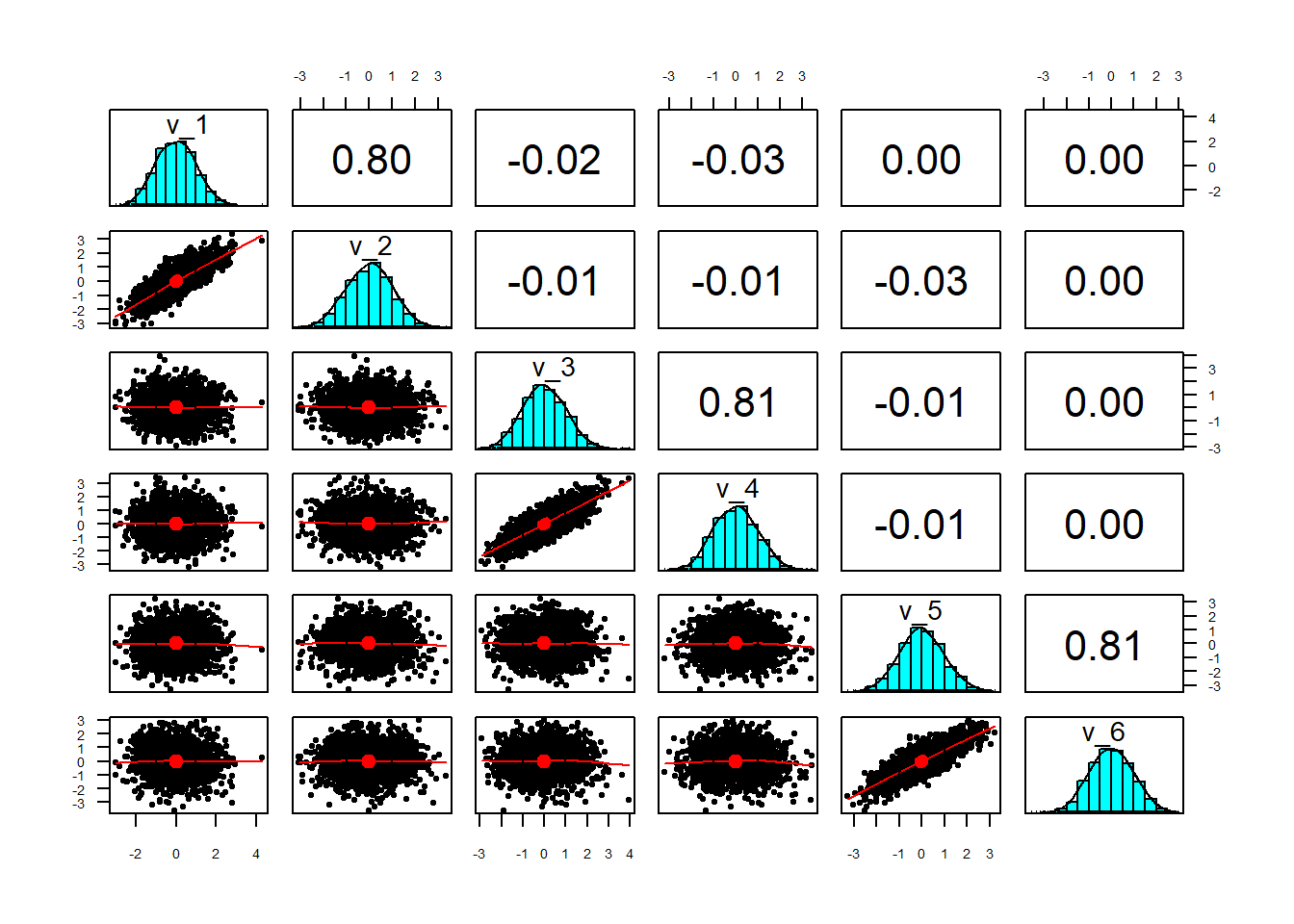
3因子の場合
| fc_1 | fc_2 | fc_3 | |
|---|---|---|---|
| v_1 | 0.9 | 0 | 0 |
| v_2 | 0.9 | 0 | 0 |
| v_3 | 0 | 0.9 | 0 |
| v_4 | 0 | 0.9 | 0 |
| v_5 | 0 | 0 | 0.9 |
| v_6 | 0 | 0 | 0.9 |
今度も極端な例です。
雑な説明をすると、V_1/2,V_3/4,V_5/6どうしだけが強い相関で
ほかは無相関というデータです。
今回は因子得点に着目します。
おそらく3因子数で因子分析をかけると
\[
因子得点1 \simeq データ1 + データ2\\
因子得点2 \simeq データ3 + データ4\\
因子得点3 \simeq データ5 + データ6
\]
みたいな関係性が得られるのではなかろうか、と。
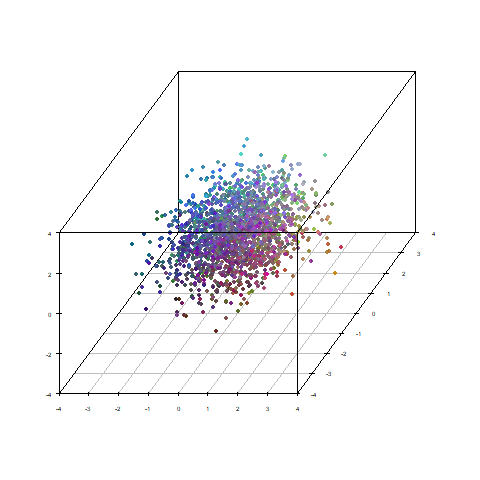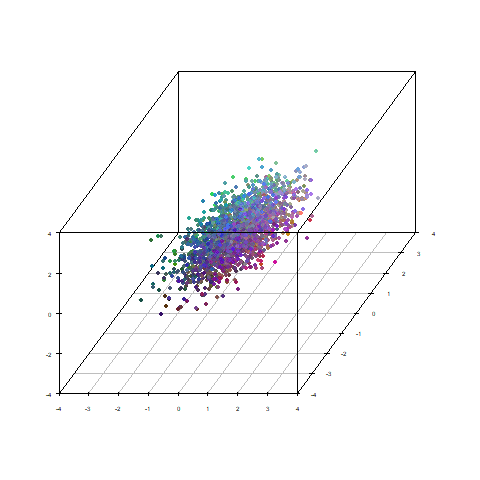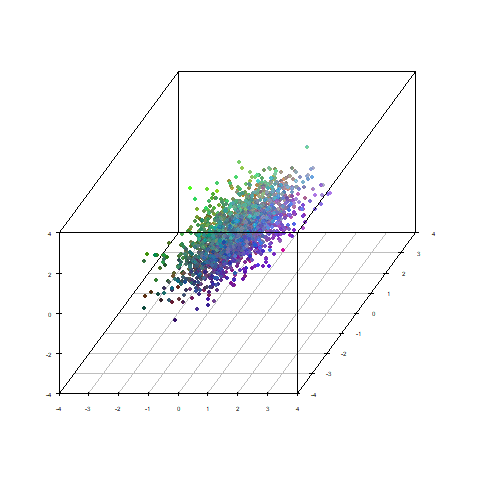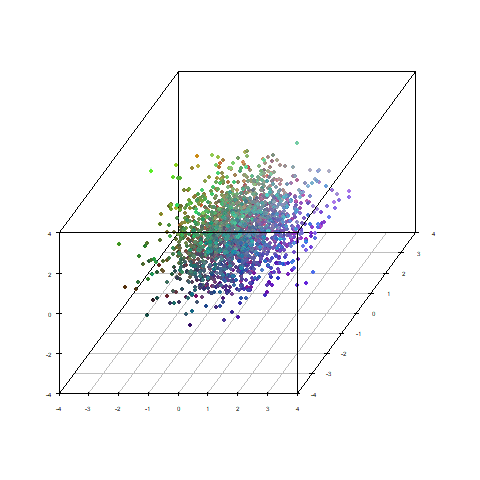
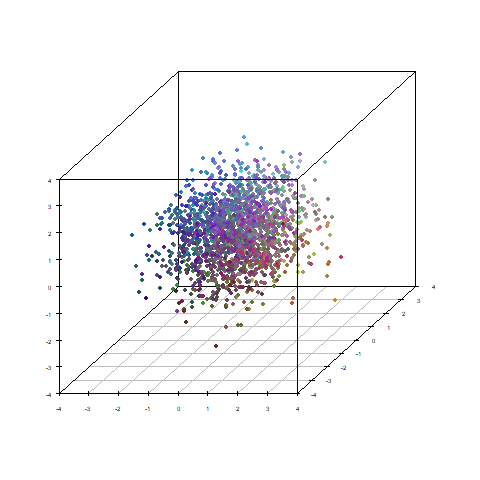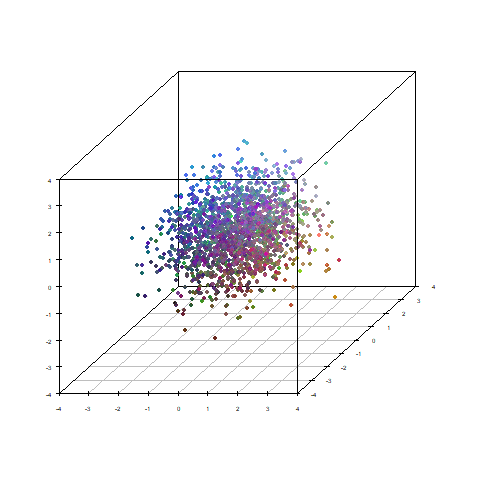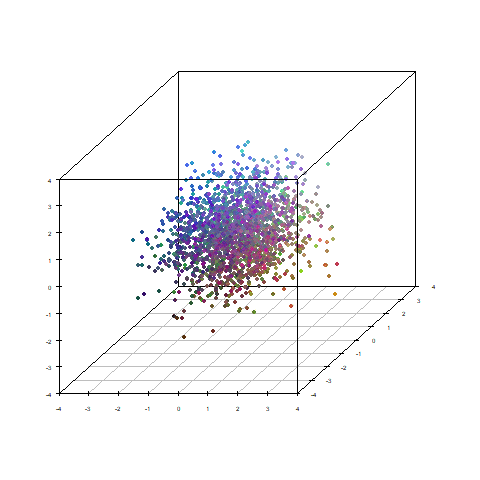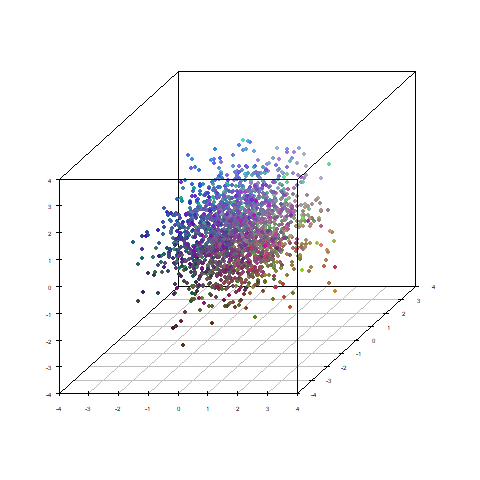
データの1,3,5列めを3次元プロットし、2,4,6列めでRGBの配色をしました。
それぞれに相関性があるので、色も位置によってグラデーションしています。
| fc_1 | fc_2 | fc_3 | Factor1 | Factor2 | Factor3 | |
|---|---|---|---|---|---|---|
| v_1 | 0.9 | 0 | 0 | 0.008 | 0.803 | -0.02 |
| v_2 | 0.9 | 0 | 0 | -0.013 | 0.997 | 0.004 |
| v_3 | 0 | 0.9 | 0 | -0.004 | -0.009 | 0.852 |
| v_4 | 0 | 0.9 | 0 | 0 | -0.009 | 0.954 |
| v_5 | 0 | 0 | 0.9 | 0.997 | -0.013 | -0.006 |
| v_6 | 0 | 0 | 0.9 | 0.811 | 0.006 | 0.001 |
先ほどと同じ表です。
先ほどと同様、因子負荷量の順序が入れ替わっておりますが
基本的な関係性が同じことを確認しました。
因子得点と元データの関係性
今回のように極端なケースであれば、因子得点と元のデータの3次元プロットは
基本似たような結果になるのではないかと考えております。
試しに元のデータから因子得点に移り変わる過程をトレースしてみます。
(ただ直線で変化つけてるだけです)
うねうねと動いて色が入れ替わっております。
これの原因は先ほども説明したとおり、因子負荷量の計算過程で
必ずしも同じ順序、符号で結果が得られない場合があることが原因です。
過去記事でも説明しました\(16 = (3×5) + 1\)でも\(16 = (-5×-3) + 1\)でも同じ16だよ
ぐらいで説明は留めます。
なので因子得点の順番を並び替えました。
先ほどのギュルーンという感じからザワザワという感じになりました。
因子負荷量ってどうやって計算するの?
元のデータと因子負荷量、因子得点などとの関係性を
何となく感じていただけましたでしょうか。
ところで、因子負荷量ってどうやって計算するの?
という疑問が浮かんだあなた、多変量解析の沼に沈みかけてます。
ちゃんと理解するには、対価として相応の人生の時間を消費することになるので
ある程度覚悟してください。
でもわかるとすっきりします。
ということで次回からはどうやって計算するの、をざっくりとご紹介します。
関連しそうなキーワード:因子負荷量、因子得点、独自性、共通性、最尤法、主因子法、確証的因子分析