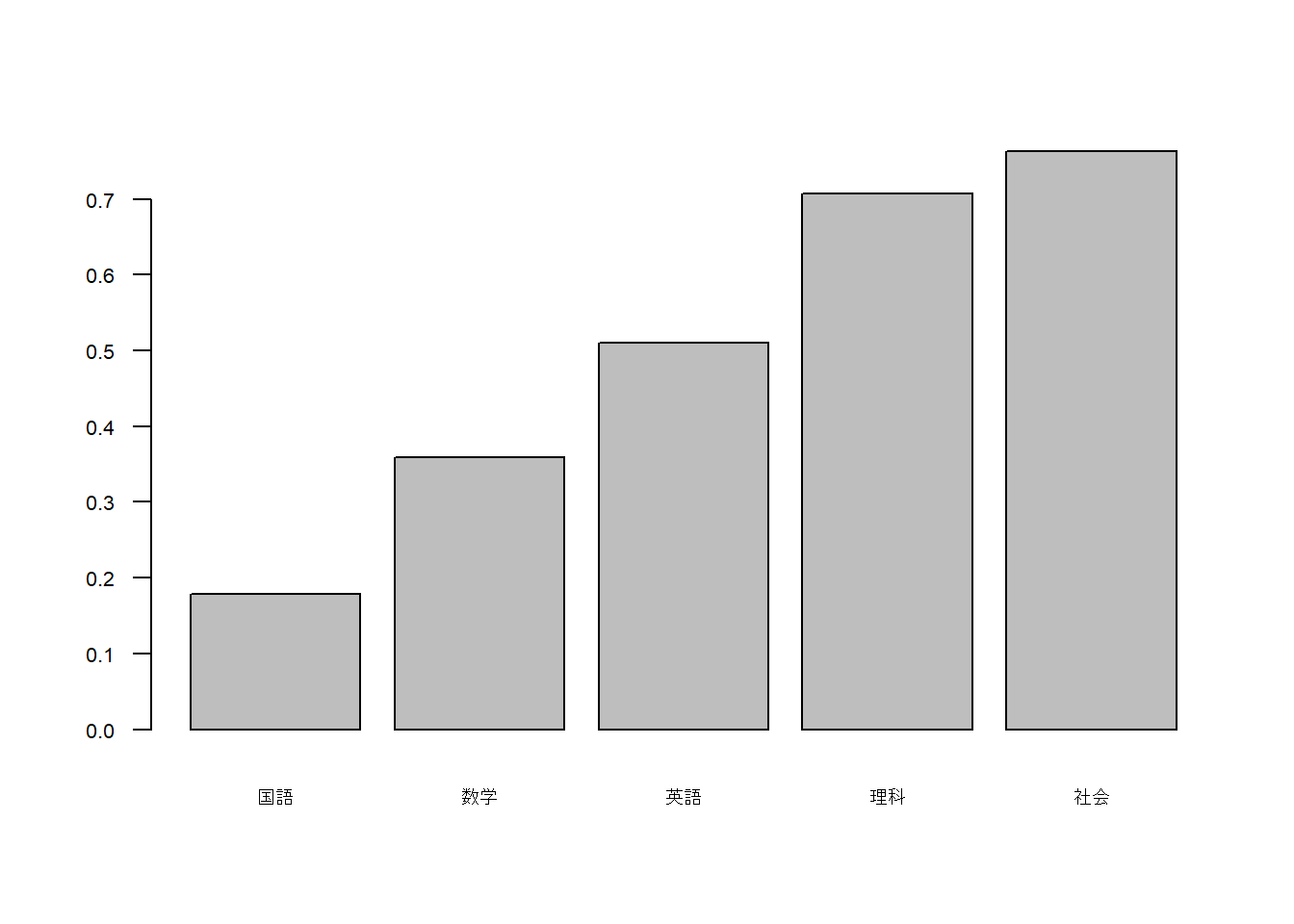ざっくり読み解く 因子分析【1因子分析編】
はじめに
ざっくり中のざっくり説明で
いくらなんでもざっくりが過ぎるぞ、というご指摘を踏まえ
もう少しだけくわしく説明するのが今回の記事です。
因子分析を難解なものにさせる大きな理由の1つが「因子数がたくさん『ある』場合」の式が複雑、という点が挙げられます。
今回は「因子数がたくさん『ない』場合⇒1因子」でご紹介しようと思います。
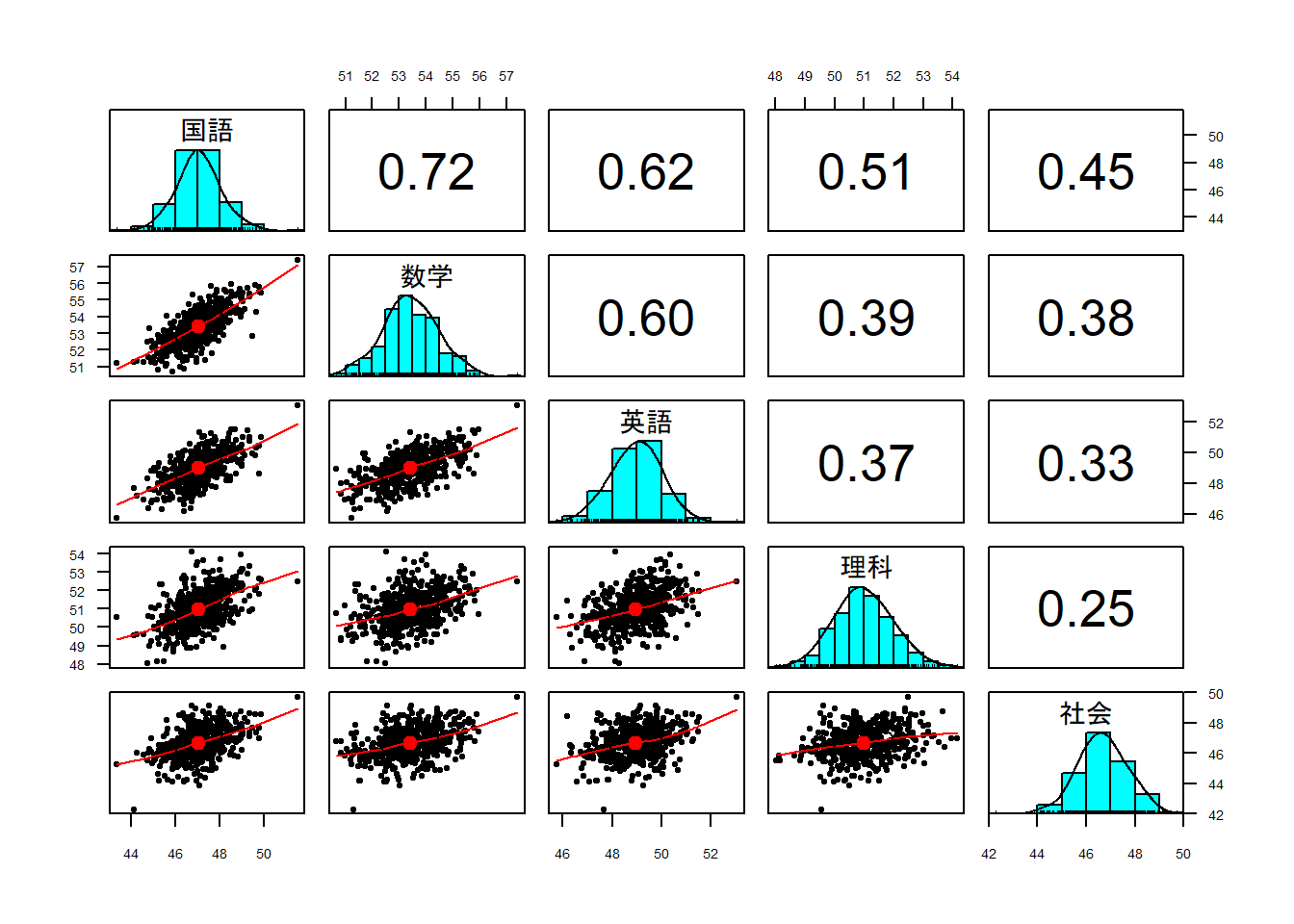
| 国語 | 数学 | 英語 | 理科 | 社会 | |
|---|---|---|---|---|---|
| 国語 | 1 | 0.723 | 0.62 | 0.513 | 0.451 |
| 数学 | 0.723 | 1 | 0.598 | 0.39 | 0.38 |
| 英語 | 0.62 | 0.598 | 1 | 0.373 | 0.328 |
| 理科 | 0.513 | 0.39 | 0.373 | 1 | 0.25 |
| 社会 | 0.451 | 0.38 | 0.328 | 0.25 | 1 |
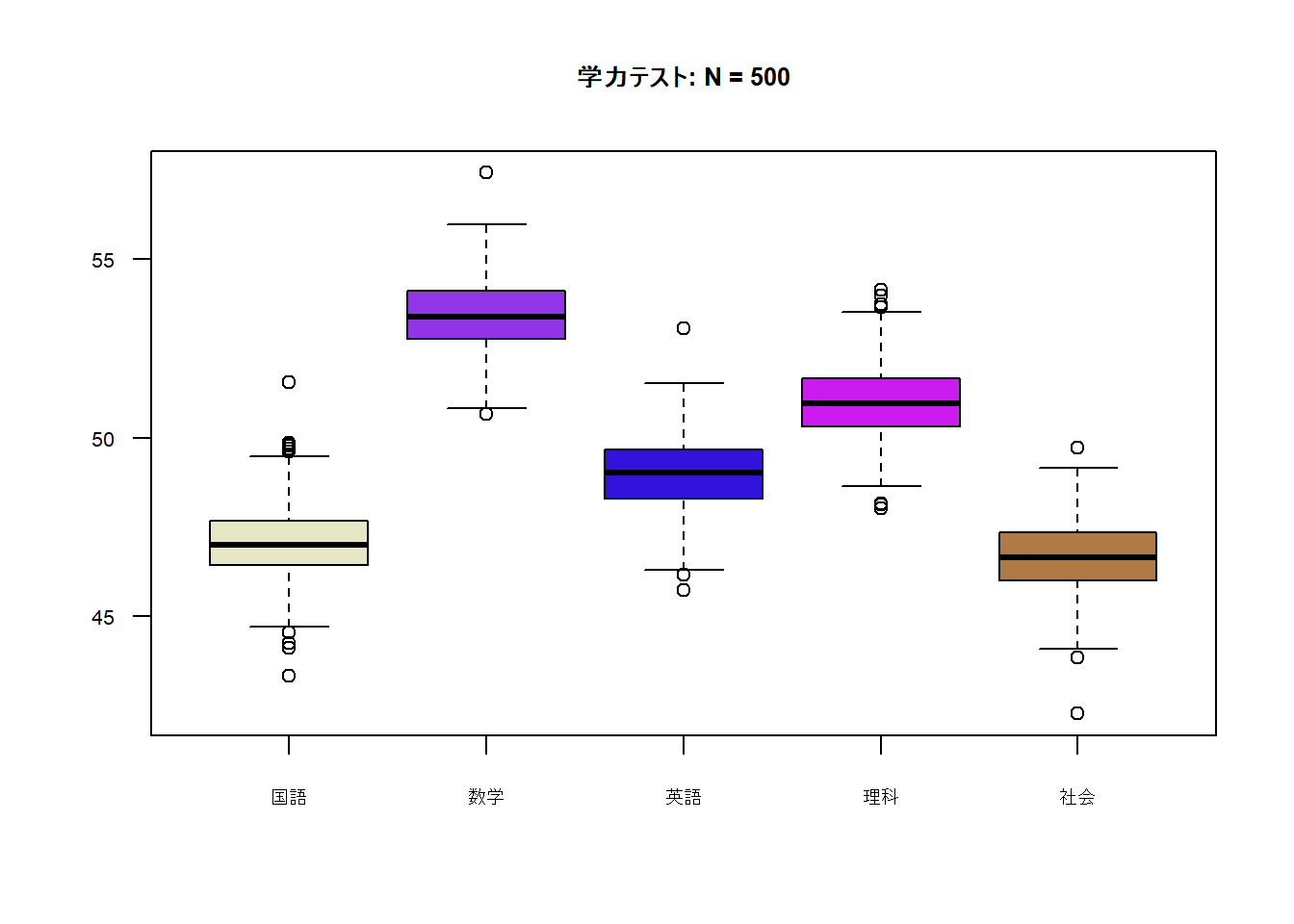
500ほどのデータで変数間の相関行列を示しました。
感の良い方ならここで気づくかもしれませんが、下記の表に似てませんでしょうか。
| 9 | 8 | 7 | 6 | 5 | |
|---|---|---|---|---|---|
| 9 | 81 | 72 | 63 | 54 | 45 |
| 8 | 72 | 64 | 56 | 48 | 40 |
| 7 | 63 | 56 | 49 | 42 | 35 |
| 6 | 54 | 48 | 42 | 36 | 30 |
| 5 | 45 | 40 | 35 | 30 | 25 |
これは5~9の掛け算表です。
じつは、先のデータはこの掛け算表をちょっと加工して乱数を生成したデータです。
完全に一致とはいきませんが、似たような相関行列となりました。
1因子分析を計算してみる
それでは作成したデータにて1因子の因子分析を行います。
| 国語 | 数学 | 英語 | 理科 | 社会 |
|---|---|---|---|---|
| 0.906 | 0.801 | 0.7 | 0.542 | 0.487 |
ピッタリ! とはいきませんが、ほぼ似たような因子負荷量が計算できました。
今回は因子分析にてセットして図示される独自性も出力します。
| 国語 | 数学 | 英語 | 理科 | 社会 |
|---|---|---|---|---|
| 0.179 | 0.358 | 0.51 | 0.707 | 0.763 |
棒グラフなどで図示する場合もあるので念のため。
ちなみに\(1-独自性=共通性\)として図示する場合もあります。
| 国語 | 数学 | 英語 | 理科 | 社会 |
|---|---|---|---|---|
| 0.821 | 0.642 | 0.49 | 0.293 | 0.237 |
個人的には独自性のほうが説明しやすいです。
ざっくり言えば「因子負荷量でうまく説明できないもの」
という感じです。
今回導出された因子負荷量をもとに掛け算の九九みたいに計算してみます。
| 国語 | 数学 | 英語 | 理科 | 社会 | |
|---|---|---|---|---|---|
| 国語 | 0.821 | 0.726 | 0.634 | 0.491 | 0.441 |
| 数学 | 0.726 | 0.642 | 0.561 | 0.434 | 0.39 |
| 英語 | 0.634 | 0.561 | 0.49 | 0.379 | 0.341 |
| 理科 | 0.491 | 0.434 | 0.379 | 0.293 | 0.264 |
| 社会 | 0.441 | 0.39 | 0.341 | 0.264 | 0.237 |
作成したデータから計算した相関行列と、ほぼ似たような結果が得られましたが
行列の真ん中の部分(対角成分)にはズレがあります。
感の良い方でしたらお分かりと思いますが、これは先ほど紹介した共通性の値と同じです。
| 国語 | 数学 | 英語 | 理科 | 社会 | |
|---|---|---|---|---|---|
| 国語 | 0.179 | -0.002 | -0.014 | 0.023 | 0.01 |
| 数学 | -0.002 | 0.358 | 0.037 | -0.044 | -0.01 |
| 英語 | -0.014 | 0.037 | 0.51 | -0.006 | -0.013 |
| 理科 | 0.023 | -0.044 | -0.006 | 0.707 | -0.013 |
| 社会 | 0.01 | -0.01 | -0.013 | -0.013 | 0.763 |
\[
対角成分(相関行列 – (因子負荷量\cdot 因子負荷量’)) = 独自性(独自因子)
\]
日本語で書いたほうがかえってわかりづらいわ!
と怒られそうですが、このあたりはもう「因子分析 詳しく」などで補完してください。
因子数を増やしていく
今回は因子数が1の場合をご紹介しました。
因子数が1の場合が何となくわかれば、複数の因子を想定した場合も基本的には同じです。
次回は複数の因子を想定した場合のご紹介をします。
関連しそうなキーワード:因子負荷量、因子得点、独自性、共通性、最尤法、主因子法、確証的因子分析