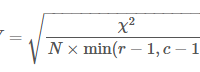【コラム】無相関について
※相関係数って何？ という記事は別記事参考ください。
相関係数は２変量間の傾向を示すために有効な手段ですが、
散布図と合わせて確認しましょう、という点は見落とされる(省略されてしまう)ことがあります。
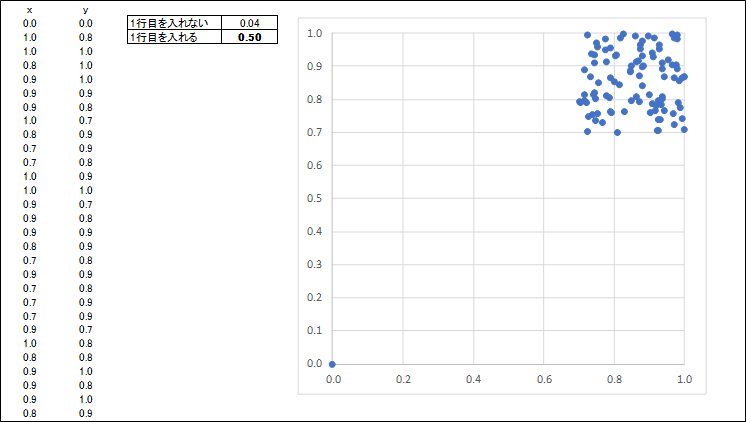
そもそも、5件法のアンケート２問の散布図となると
取りうる値は25通りしかなく、散布図で示すとこんなことになってしまいます。
もちろんこれでは何がなんだかわかりませんので
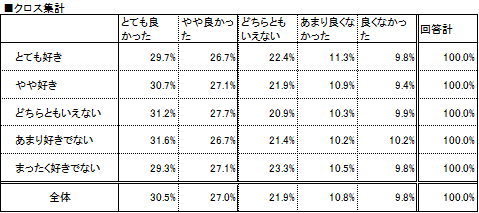
一般的にはクロス集計や帯グラフだったり
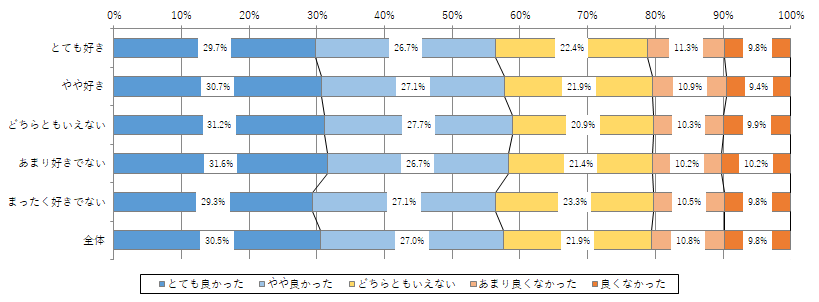
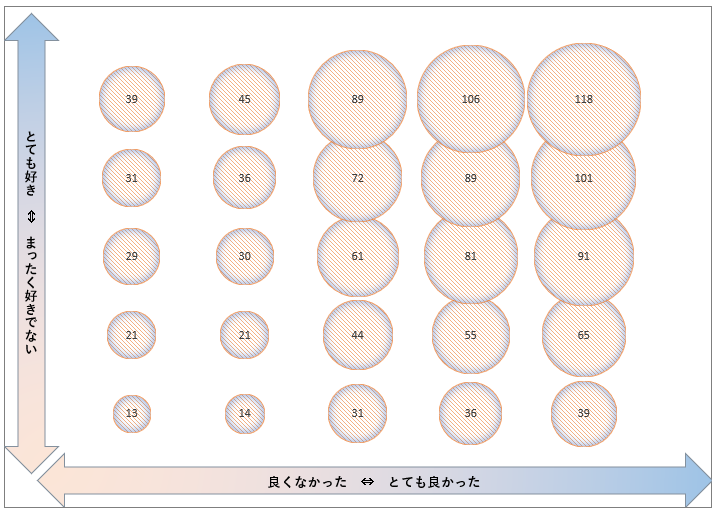
頑張って散布図で示すならバブルチャートだったりと
やり方がないわけではないのですが、もう少しバラついた情報であったとしても
特定の情報に視点を絞ってしまうと、読み違えてしまうことがあるのではないか、という話題です。
例1、相関があるように見えるけど、全然意味がない散布図
相関係数はほんとうにざっくり言えば、右肩上がりか左肩上がり、何れかになっていれば顕著な傾向が得られます。
アニメーションのとおり
・右上に向かっているうちは顕著に正の相関
・左上から右下に線がクロスすると無相関となる
・ところが同じクロスが離れた右上に出現すると、再び強い正の相関となり
・同じものが離れた左上、右下に出現すると、また無相関となる
ここまで極端な事例は社会調査で起きることはないと思いますが
ある特定の傾向に対して真逆の受け取り方をするグループ、
例えば甘党と辛党の両派閥に塩キャラメルを食べてもらったとき
甘み0～100まで変化(x軸)をさせれば、両グループの「美味い！」評価の変化(y軸)は交差するのではないでしょうか。
その場合、やはり甘党と辛党の両方のデータを一つの散布図に入れれば無相関になるでしょうし
甘党だけであれば正の相関、辛党だけであれば負の相関になると想像できます。
例2、無相関の検定が「有意であれば相関がある」の落とし穴
無相関の検定の細かい話は省略しますが、大まかには
傾き（相関係数）が乱数では起き得ないぐらい（有意に）傾いていれば
無相関ではない（棄却される）ので相関性がある（のではないか）。
といった具合です。
それそのものの理屈について何を言える、ということもないのですが
問題は
・有意ってどの程度で？
・回答数（N）の影響は？
という点に留意しての使用が推奨されます。
有意ってどの程度で？
まず、有意というものを少しだけ整理します（≠学術的）。
もちろん、言葉通りに意味が有る、ということになりますが
仮説検定では「偶然では起き得ない⇒必然」というニュアンスで使われることが多いと思います。
つまり偶然や必然というものは確率論的な話題になるので、0%～100%の間で揺れる何かの値が
定義した発生率を下回れば偶然じゃ考え難いねこれは、ということになり、必然として扱われます。
（帰無仮説とか第一種の過誤とか、そういうのは適宜ググってください）
では「定義した発生率」とはなんだ、という話ですが
結論から先に書いてしまうと、個人的な調査であれば、自分が有意だと思った範囲で良いかもしれません。
もちろんそんな主張が対外的に認められることはないので、
論文などでは5%未満などが多いと思います。
で、この5%未満というのは乱数であっても20回に1回は得られる現象、というのがポイントです。
回答数（N）の影響は？
仮説検定全般に言えることですが、N数の影響を大いに受けます。
つまり、Nが増加するとちょっとした差でも有意じゃん、ということが多くなります。
※そもそもN数がたくさん取れないから使うのですが。
あまり細かく説明すると長くなるので
・一様分布で生成した２変量（どうあっても無相関）のデータを
・同じN数で何回も繰り返して（試行）有意水準（<0.05）を下回ればループ離脱
・N数を増やしていくとより無相関らしさが際立つが、試行回数は増えやしないか
・ついでに単回帰係数を出して直線を引く
という検証アニメーションです。
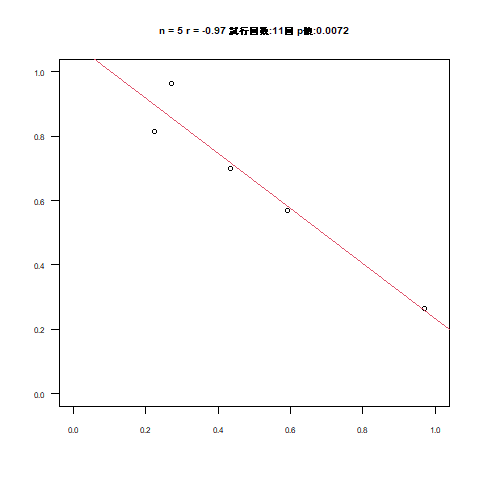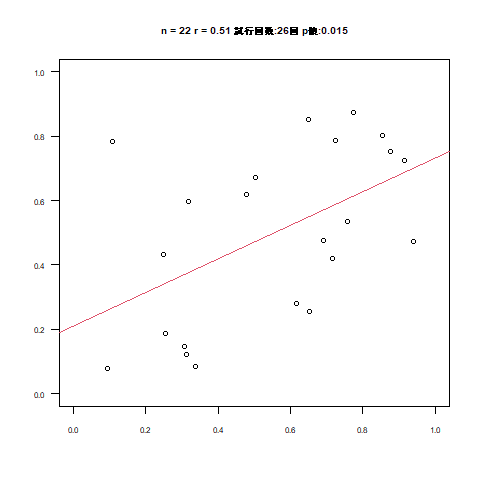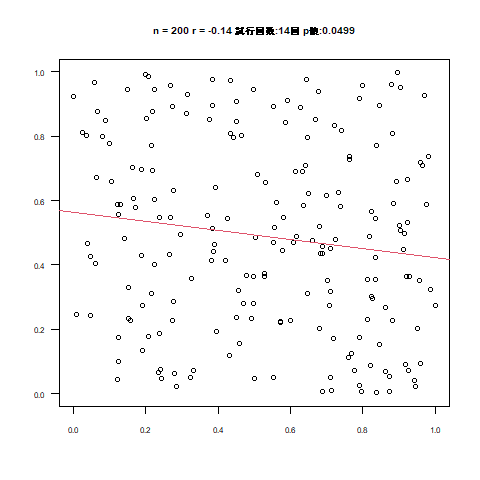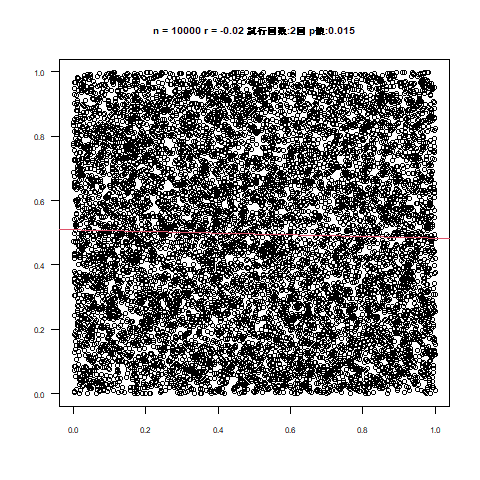
試行回数の箇所を目視いただくと大体1ケタ台から多くて40回程度かと思います。
同じアニメーションの処理を数十回やったところ、大体試行回数の平均は20回くらいで収まりました。
※Rでmean(rexp(n = 10000,rate = 0.05))を走らせても20くらいになります。
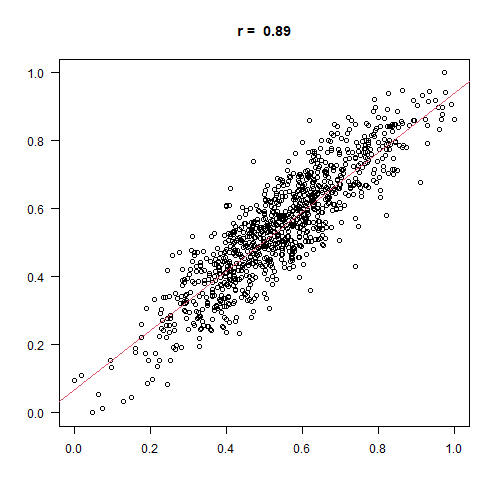
しかし散布図を見てもN数が30超えたあたりから散布図そのものに直線らしさがなくなります。
それもそのはずで、N数が増加するほど傾きが下がっていきます。
それでも無相関の検定手法的には有意水準を下回る⇒関係性がある、と読めてしまうわけです。
※下のアニメーションはNの増加に合わせて有意水準(0.05)を下回る相関係数の値が下がることが確認できます。
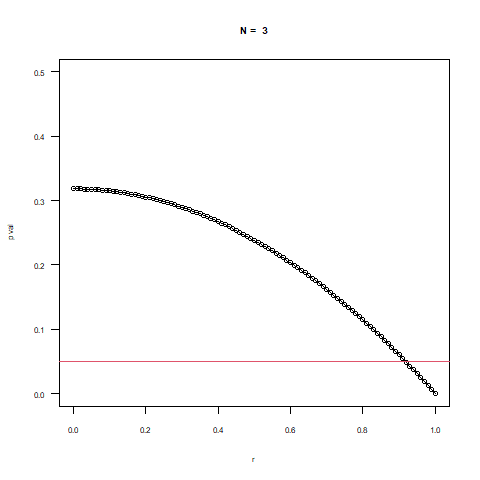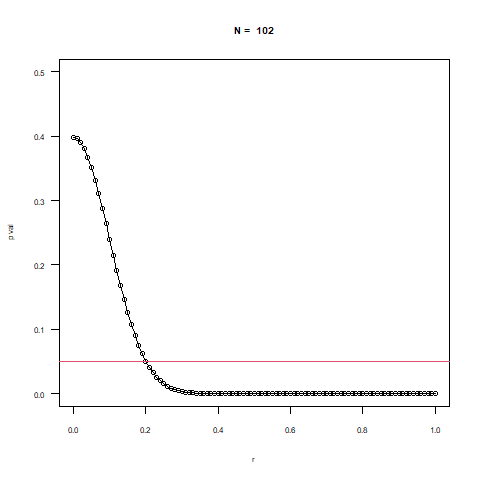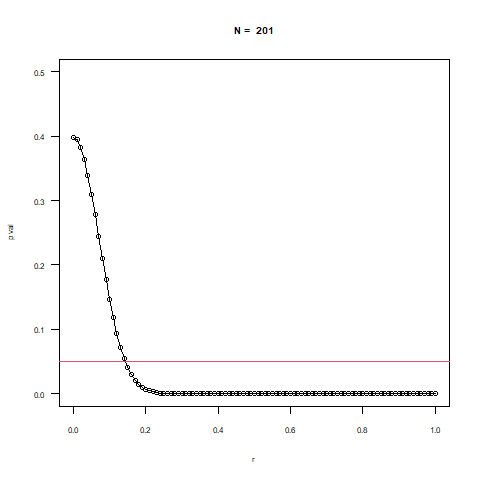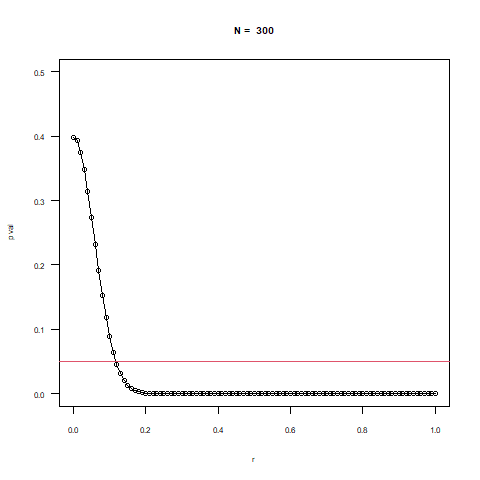
三次元的に示すと上の図のようなイメージです。
小さいN数であれば相関係数が高くても有意水準を下回らない範囲が多くなりますが
Nの増加に伴って急激に幅が狭くなることがわかります。
過去にも悪用厳禁のネタはいくつか出しておりますが
有意水準に着目し、有意な結果が得られた⇒無相関が棄却されるので相関性（関係性がある）と
どのような結果に対しても述べてしまうことの危険性を再認識しました。
ついでに
欠損の扱いを「0」で処理するケースをたまに見ますが、たった1レコード0があるだけでも
相関係数はこんなに変わります。
※もちろん悪用厳禁です。
