ポアソン分布について|Excel(エクセル)で学ぶデータ分析ブログ
ポアソン分布とは?
Wikipedia より(一部編集)
統計学および確率論においてポアソン分布 (Poisson distribution)とは、数学者シメオン・ドニ・ポアソンが1838年に確率論とともに発表した、所与の時間間隔で発生する離散的な事象を数える特定の確率変数 X を持つ離散確率分布のこと。
ポアソン分布の仕組み
ポアソン分布は二項分布を極端に考えたときの確率分布と説明されることが多いです。
\[
p(X=x) = {}_nC_x p^x (1-p)^{n-x}
\]
二項分布では、確率pの事象をn回試行したときの結果xを予測することができました。
例えばサイコロの1をアタリと定義して1,000回ほど振ってみると
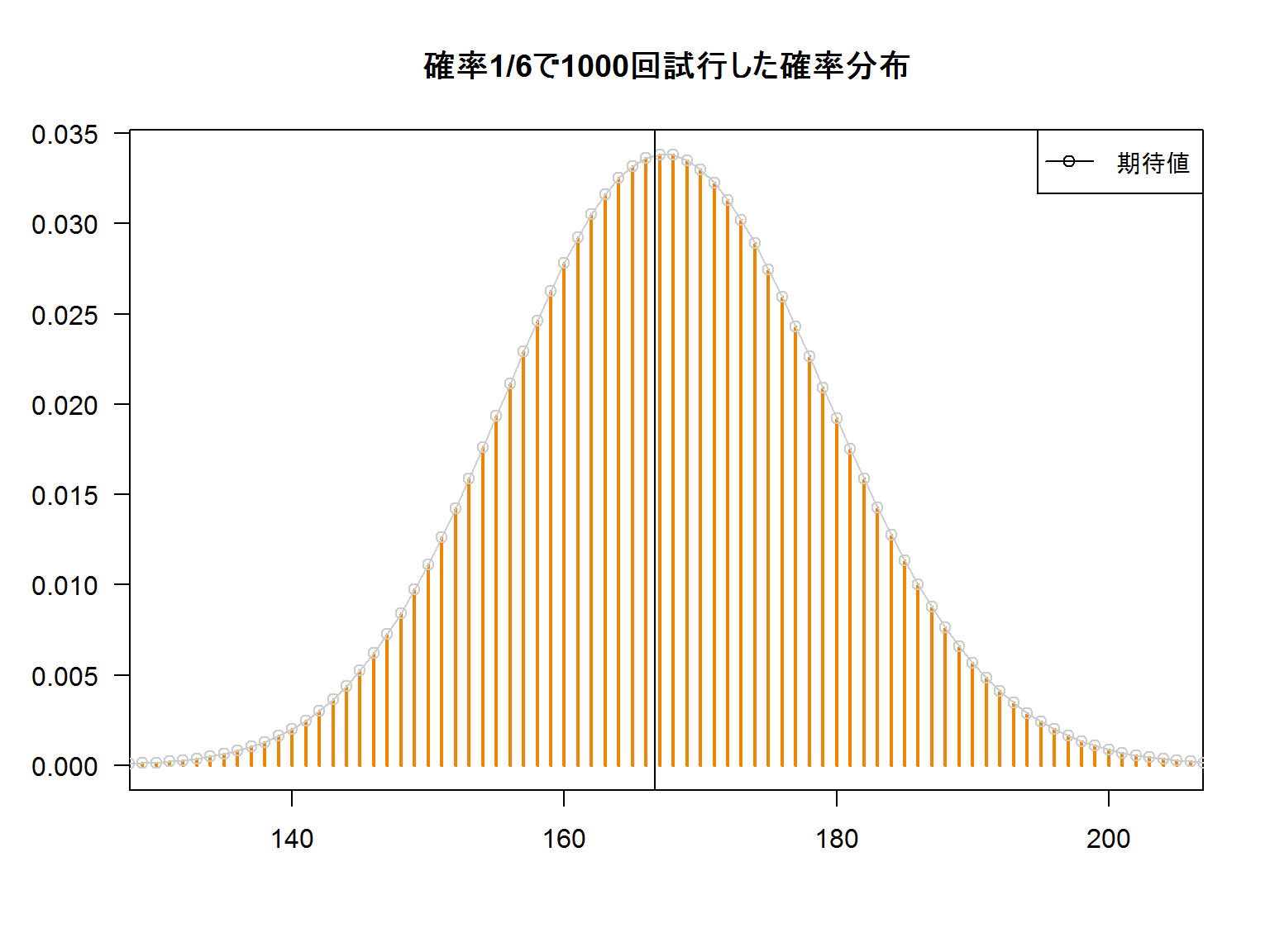
おおよそn*p≒166回程度1が出ることが予想されます。
ここでnp=166を一定(\(np \to \lambda = 166\))にし、且つnを無限(\(n \to \infty\))にしていきます。
nを無限にするということは「試行回数」という考え方から視点をずらすようなイメージです。
サイコロで例えることが難しいので、お店の来客数で例えます
「だいたい毎日166人くらい来客あるよね」という感じです。
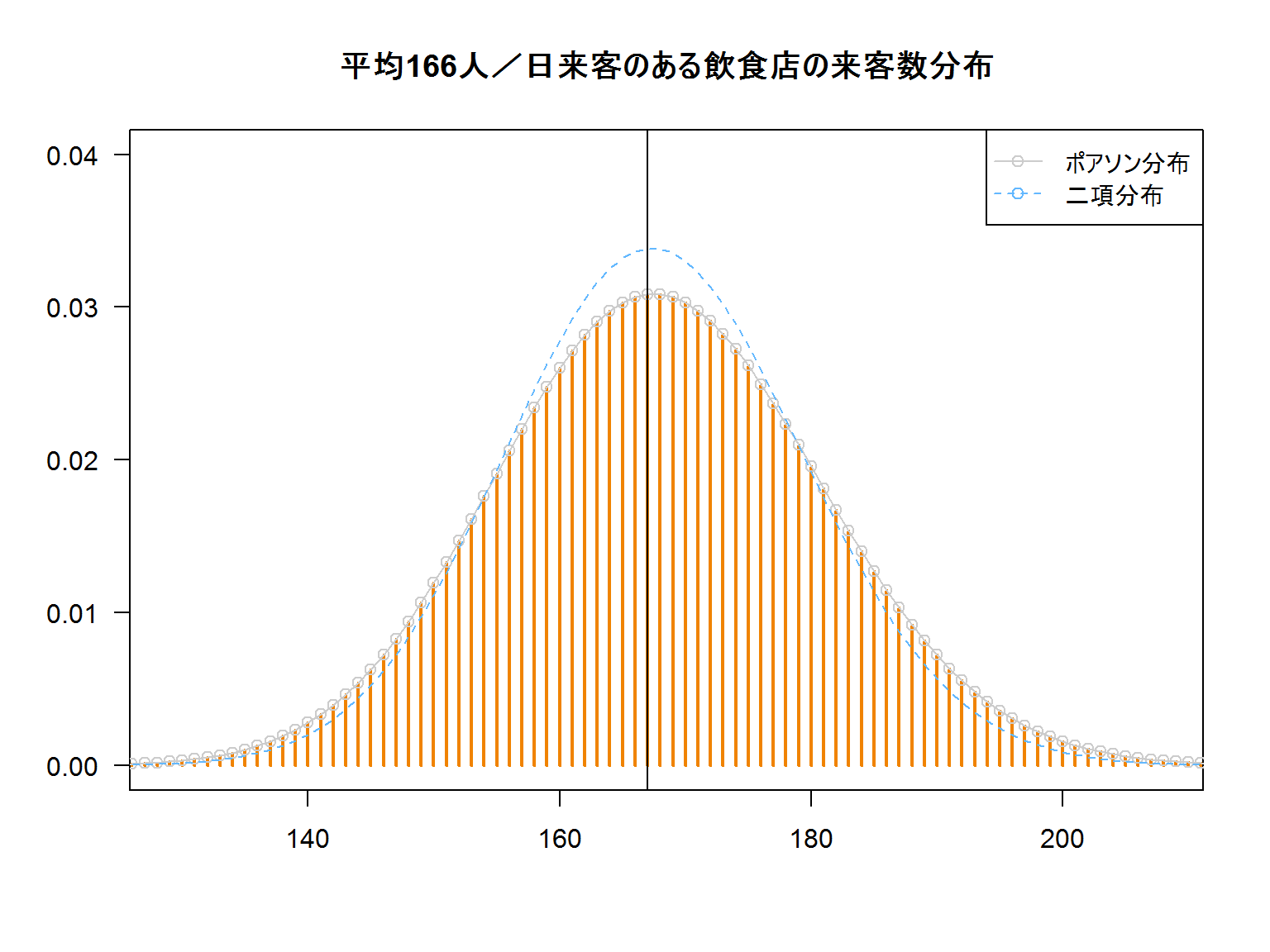
\[
P(X=x)= e^{-平均来客数} \frac {{平均来客数}^x}{x!}
\]
\[
P(X=x)= e^{-\lambda } \frac {\lambda^x}{x!}
\]
乱数のシミュレーション
1日あたり166人来る飲食店を乱数でシミュレートしました。
n*pを一定にしながら数千回施行を繰り返します。
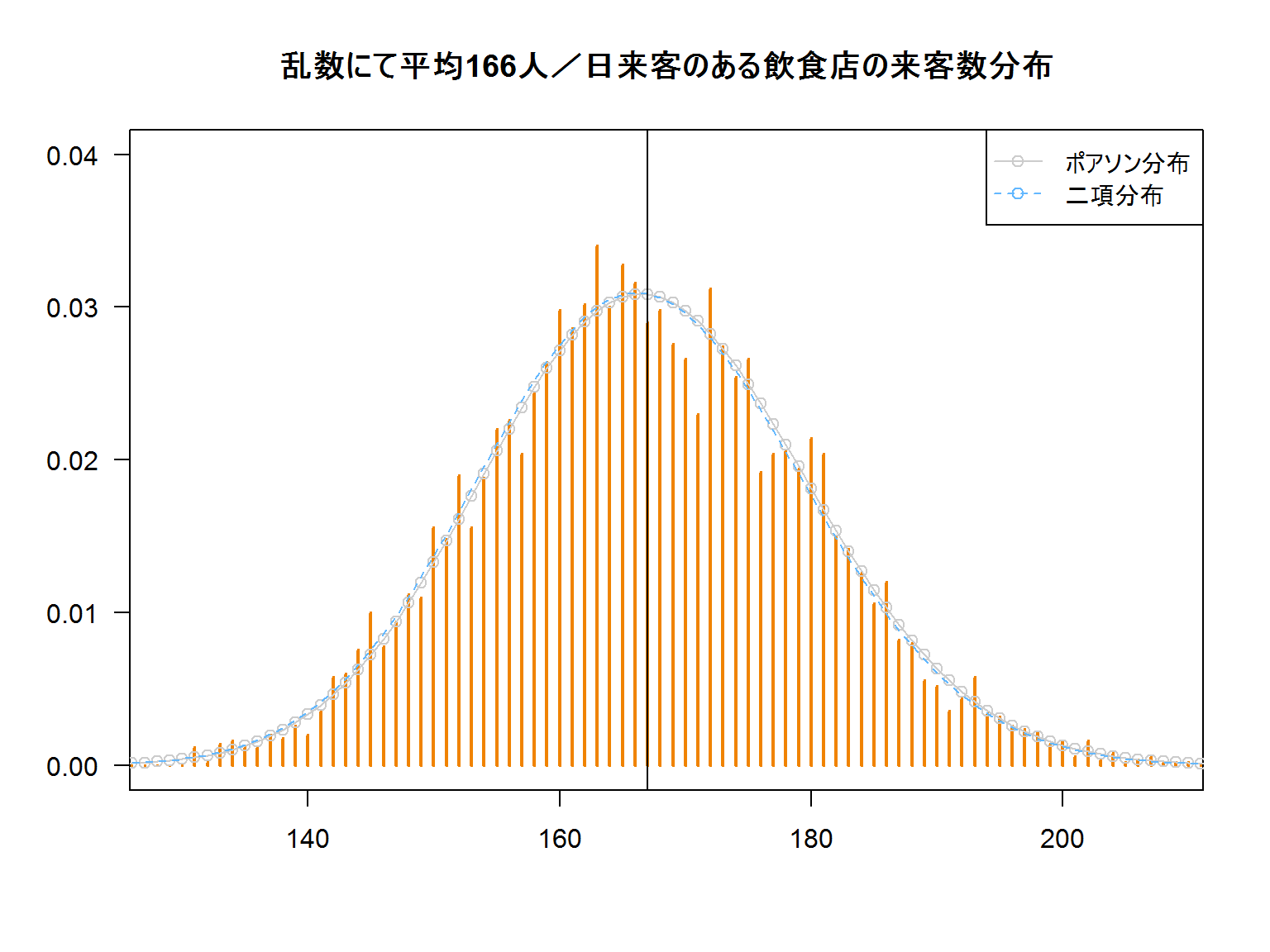
エクセルでは下記のようにあらわします。
=EXP(-B$1)*((B$1^$A2)/FACT($A2))=POISSON.DIST($A2,B$1,0)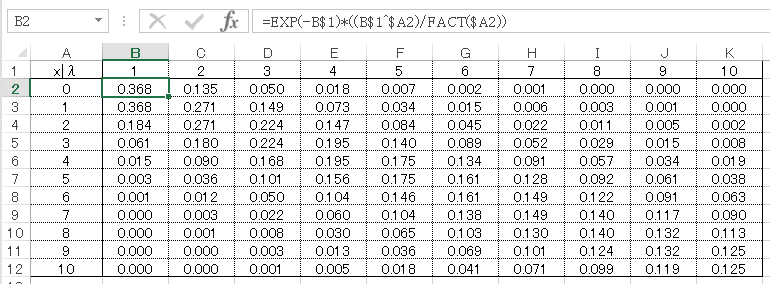
ポアソン分布の正規近似
期待値が一定量を超えてくると、期待値=分散の正規分布に近似してきます。
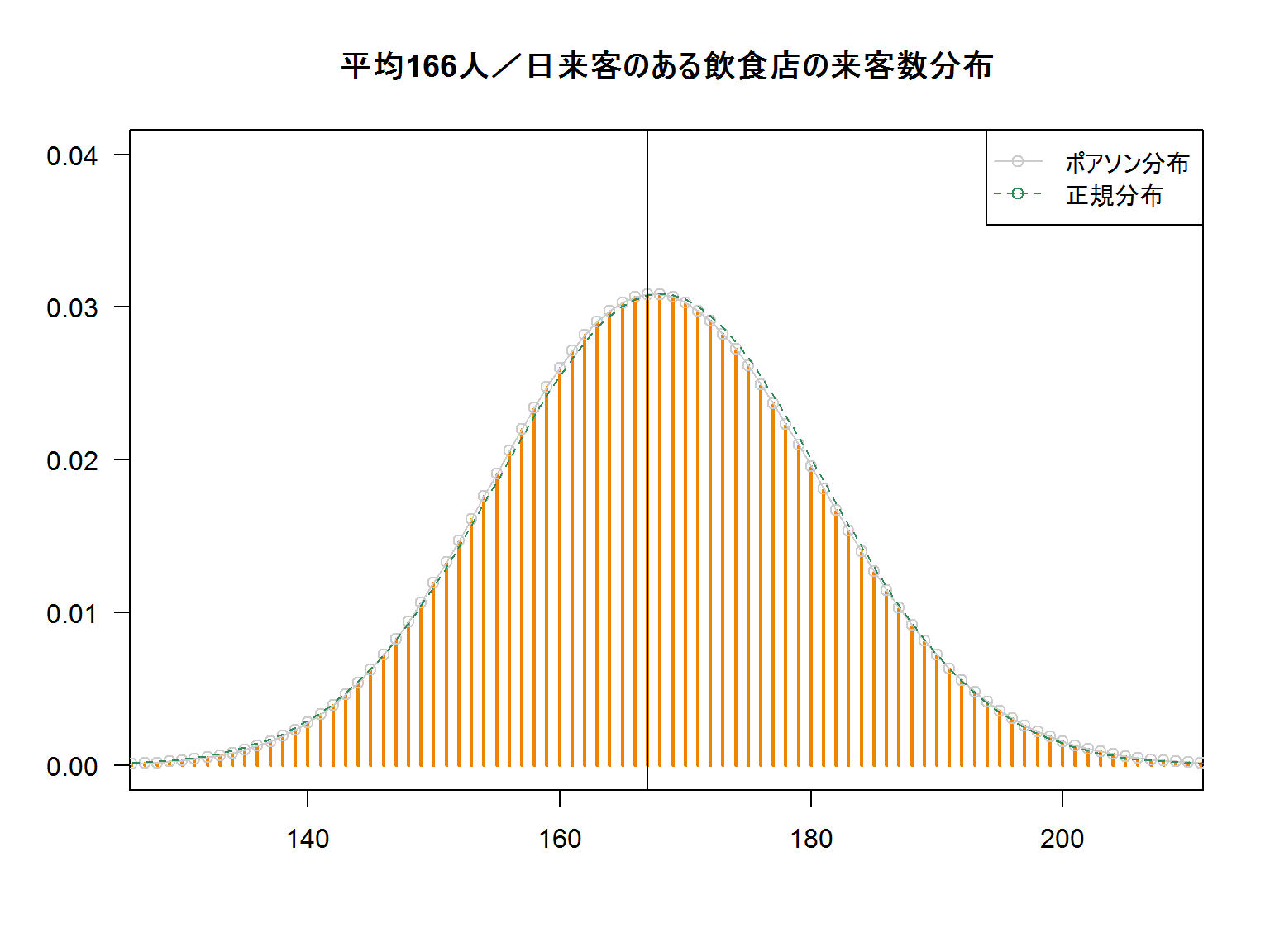
但し期待値が低い付近だと当然のことですが正規分布はマイナスを示します。来客数がマイナス5人だ、というのはありえないですね。
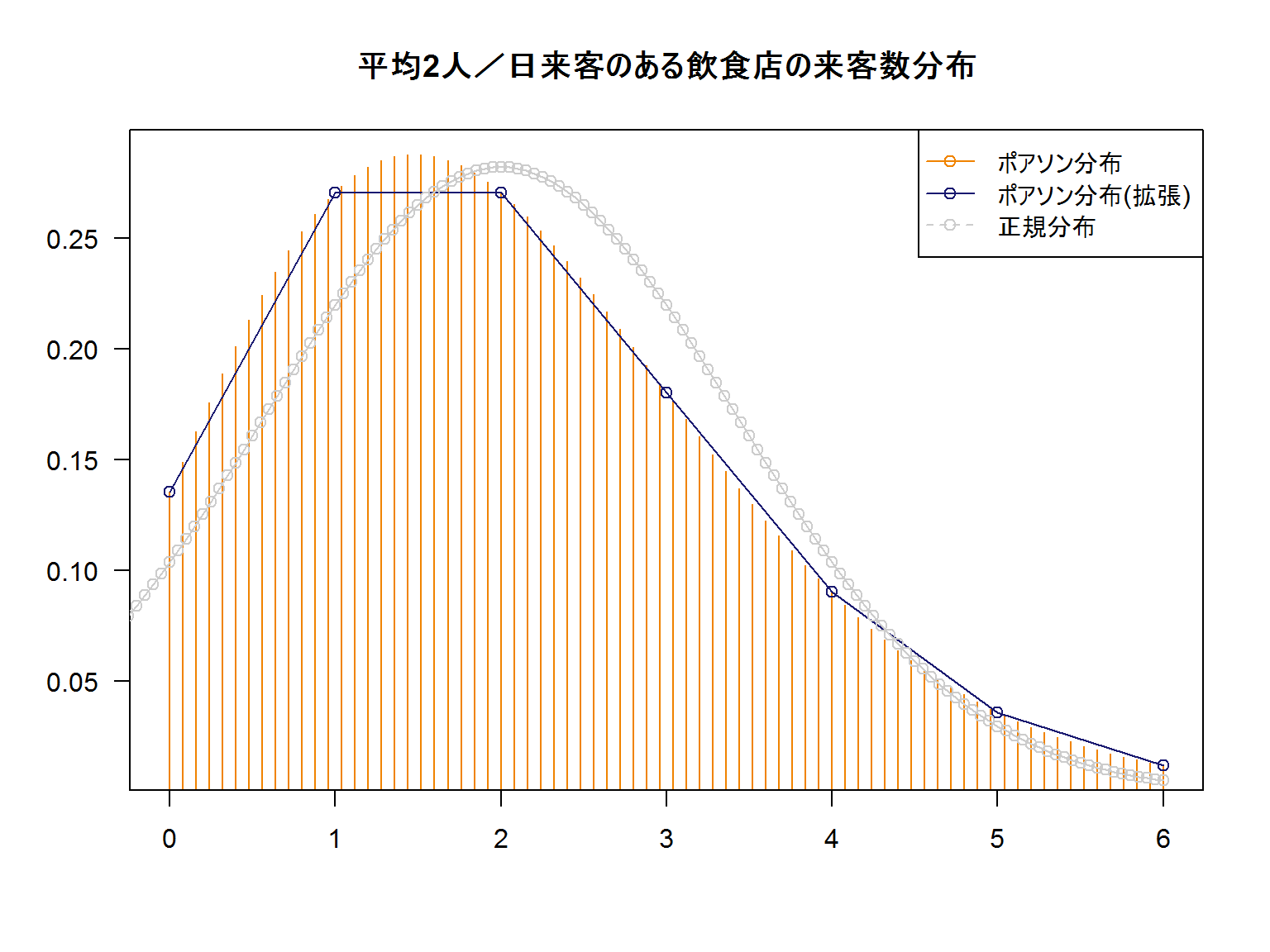
ポアソン分布の数式には階乗が含まれているのでガンマ関数で拡張し連続性を出してみました。
このように期待値が低い=「めったに起きない」事象を扱う際に効果を発揮するのがポアソン分布です。




