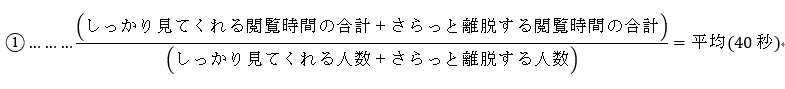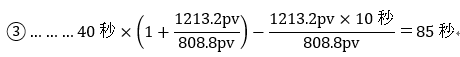【コラム】WEBアクセス解析による本当の閲覧時間の推測|Excel(エクセル)で学ぶデータ分析ブログ
■WEBアクセス解析による本当の滞在時間の推測
先日、事務所の打ち合わせでとあるページの滞在時間を眺めておりました。

スタッフA「これだけの期間でたくさんの人に見てもらえたんですね」
筆者「ありがたいですね。もっとわかりやすい記事を考えないと」
スタッフA「ほんとですね」
筆者「でも私の記事ってつらつら長いのに40秒で読めるもんなんですかね?」
スタッフA「まぁ平均ですから。6割ほどは10秒くらいで離脱してるアクセスじゃないですか。既読者とかスパムなんかだともっと短いでしょうし」
筆者「じゃあ、その影響を取り除いたらしっかり読んでいただいてる方の平均時間が推測できるんじゃないですか?」
ということで情報を下記のとおり整理してみましょう。
■とある影響を取り除いた平均値を計算してみる。
まず、平均ってなんぞや、というところですが
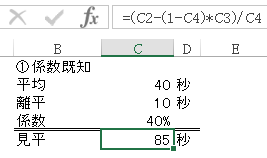
平均=閲覧時間の合計/母数=40秒となります。
この閲覧時間の合計/母数という式を下記のように分解してみましょう。
で、目的はこの中から「しっかり見てくれる人の平均閲覧時間」を抜き出せばいいわけですね。
細かい証明はいろいろ突っ込まれたりしてモチベーションが下がるので、筆者が導出した結果だけ記載します。
文字が長いので下記の略号を用います。
・見平:しっかり見てくれる平均閲覧時間
・見数:しっかり見てくれる人数
・離平:さらっと離脱する平均閲覧時間
・離数:さらっと離脱する人数
こんな結果が出たので、下記の値を代入します。
スタッフA「まぁ平均ですから。6割ほどは10秒くらいで離脱してるアクセスじゃないですか」という発言から
・離平=10秒とします。
たぶん平均値はページビュー数(pv)から計算してると思うので
・離数=2022×0.6=1213.2pv
・見数=2022×0.4=808.8 pv
で計算してみましょう。
ということで、しっかり見てくれる平均閲覧時間は85秒となりました。
もちろんこの中でも長い方短い方がいるし、そもそも根拠の無い係数ではありますが、
なんとなく経験則から考えても合致していそうな気がします。
■もっと便利な式にしたい。
②の式はややこしいですね。なんで1を足すのかわけがわかりません。
と計算しながら思いました。
待てよ、「しっかり:さらっと」の対比構造であれば、わざわざ母数を組み込む必要があるのだろうか。
何が言いたいかというと、離数と見数を計算せずに、「しっかり:さらっと=0.4:0.6」の構造をそのまま利用すれば
計算が簡易になるのではないでしょうか。
ということで、ページビュー数の2,022を「N」、見る人係数を「a」として表現をすると下記のように整理ができます。
・離数=N×(1-a)
・見数=N×a
これを②に代入して計算をすると下記の結果を得ることができました。
なんということでしょう。計算過程でNが消えてしまいました。
こっちのほうが使い勝手がいいですね。
「平均40秒か。6割は10秒くらいのショートアクセスだから
読んでくれる人のアクセスでは平均85秒くらいで見てくれているんだろうな(キリッ」
なんだかできるWEBアクセス分析者の匂いがしてきました。香ばしいです。
■応用も利くんじゃないか?
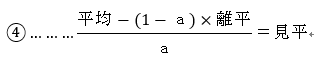
この式はしっかり見てくれる平均閲覧時間を推測するために用いましたが、
逆に記事の文量から「これくらいは読むのに掛かるだろう」という時間を予想し、それに合致した比率の計算も可能となります。

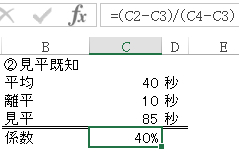
見平=2分=120秒として計算してみます。
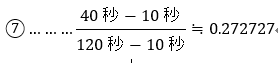
ということで、
・離数=N×(1-a) =2,022 pv×(1-0.272)≒ 1,472 pv
・見数=N×a=2,022 pv×0.176 ≒ 550 pv
となりました。全体の70%以上がショートアクセスということになり、しっかり見てくれるアクセスは全体の30%以下。
どちらを信じるかは、経験則に委ねられますが、WEBのように不特定のショートアクセスが入るような平均値には有効な計算方法ではないでしょうか。
■エクセルでも計算してみる。
無理やり感はありますが、当記事はエクセルで作業をすることに拘りがあるので計算も載せておきます。
①係数を予想した場合の平均時間
②平均時間を予想した場合の割合
記事別にガーッと計算してみると案外長く読まれているのは別記事だったりと結果が見れて面白いかもしれません。