ざっくり読み解く 因子分析【ざっくり中のざっくり編】
はじめに
過去に紹介してきた主成分分析や重回帰分析と比べ
因子分析のざっくり解説の難易度は高いという心象です。
それは主成分分析や(一般化線形モデルという意味でない)重回帰分析が
誰がやっても計算結果が(計算誤差を除けば)同じであることに対して
因子分析は掛けるパラメータ、処理法などによって様々な結果が得られるためです。
因子分析とは
「おれ、理系だからサ」とか「文系ですので」とか社会人になっても度々耳にします。
または「理系も突き詰めると文系だよネ」とか、またはその逆の用法とか、聞く機会もあるのではないでしょうか。
| 国語 | 数学 | 英語 | 理科 | 社会 |
|---|---|---|---|---|
| Min. :53.52 | Min. :48.07 | Min. :55.44 | Min. :48.16 | Min. :56.76 |
| 1st Qu.:55.70 | 1st Qu.:50.12 | 1st Qu.:58.20 | 1st Qu.:49.87 | 1st Qu.:59.10 |
| Median :56.33 | Median :50.83 | Median :58.91 | Median :50.59 | Median :59.77 |
| Mean :56.34 | Mean :50.83 | Mean :58.85 | Mean :50.58 | Mean :59.73 |
| 3rd Qu.:56.98 | 3rd Qu.:51.53 | 3rd Qu.:59.47 | 3rd Qu.:51.24 | 3rd Qu.:60.39 |
| Max. :59.45 | Max. :54.14 | Max. :61.68 | Max. :53.34 | Max. :62.74 |
500ほどのデータで統計量を出すとこのような感じです。
ところで、いわゆる「理系」とか「文系」というのはどういうものを指すのでしょうか。
とりあえず計算
直感でいえば
国語や英語や社会が得意であれば「文系」ですし
数学や理科が得意であれば「理系」なのだと思います。
もちろん世の中には社会と数学がめちゃくちゃ得意な子や
そもそも英語圏で育った子が理科好きであれば英語と理科が得意、ということになると思います。
| Factor1 | Factor2 | |
|---|---|---|
| 国語 | 0.8002 | 0.1393 |
| 数学 | 0.06258 | 0.9955 |
| 英語 | 0.6882 | 0.3944 |
| 理科 | 0.2534 | 0.6406 |
| 社会 | 0.9087 | 0.08994 |
今回収集したデータにて、2因子を指定し因子分析を掛けると上の結果のようになりました。
単純な大小関係でよいのですが
Factor1は国英社、Factor2は数理と関係性が強いように感じます。
このように、ある変数を指定した因子数で分解したものを「因子負荷量」と呼びます。
\[
x(データ) = \lambda(因子負荷量) + e(説明できないもの)
\] 正しくは平均値を考慮したり数式に詳細な補足説明が必要ですが
今回はざっくり中のざっくりで説明してますので
詳細は別記事でご紹介しようと思います。
詳しく知りたい方は「因子分析 詳しく」などでぜひ検索してみてください。
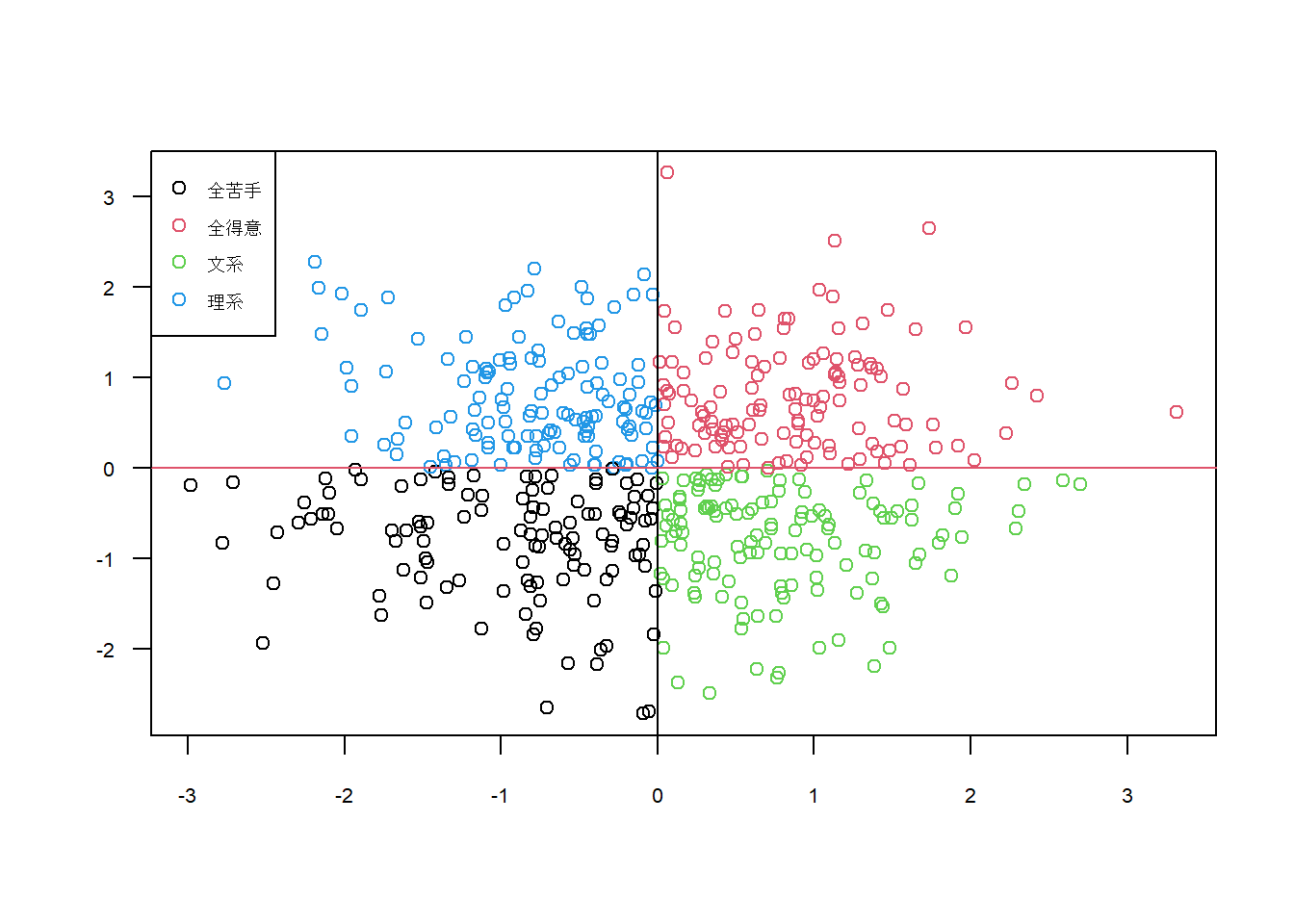
因子負荷量をもとに因子得点(\(f\))というものも計算できます。
文系や理系同様に、どちらも得意またはどちらも苦手な学生も当然いるわけです。
この散布図はそれらを極力均等に配分しました。
それらのグループ情報を、もとのデータに反映し確認しました。
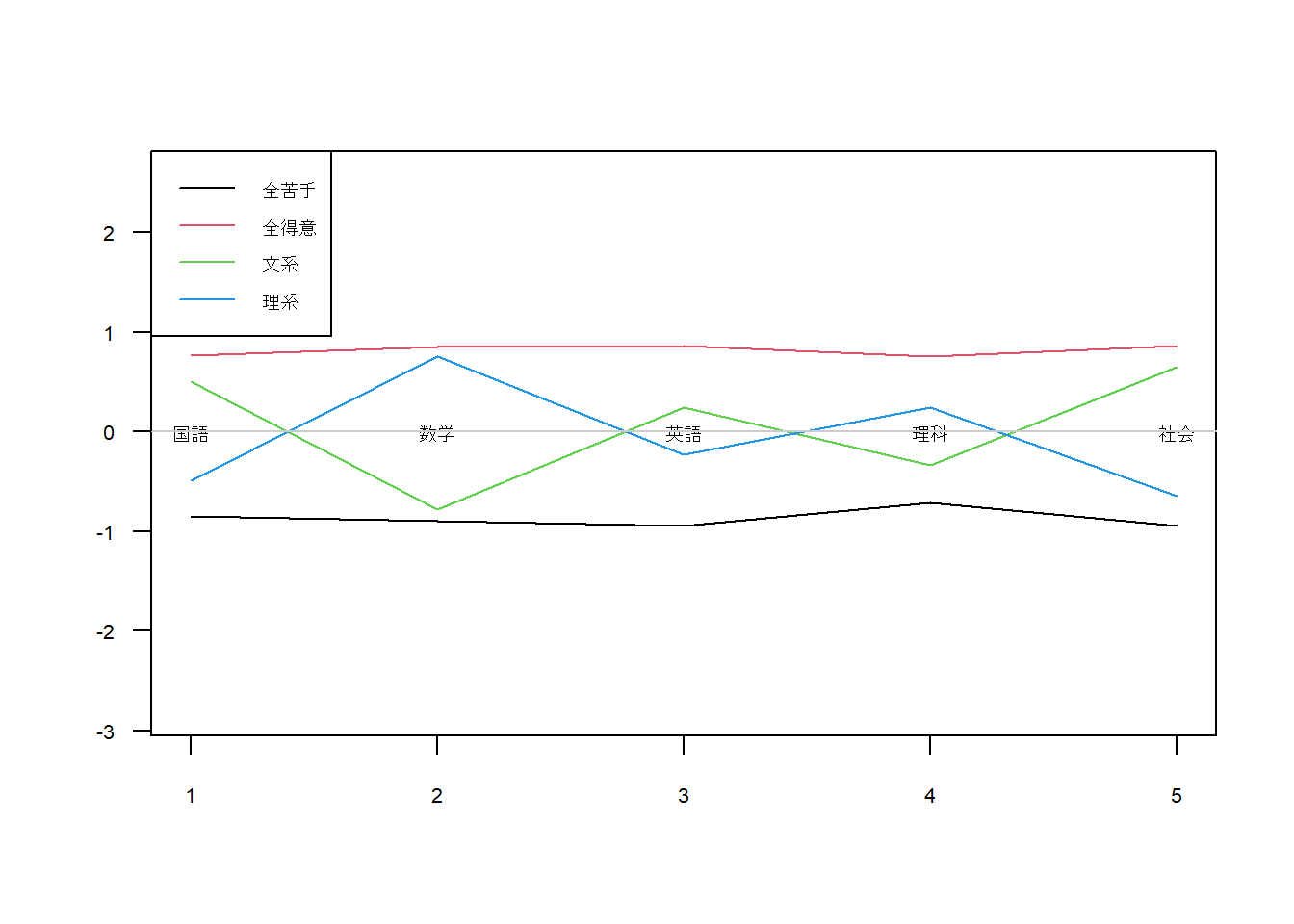
ちょっと違いがわかりづらいので平均値を0に変換します。
それぞれのグループが、それらしく判別できていることが確認できました。
因子分析を使いこなしたい
前述のとおり、因子分析は重回帰分析や主成分分析と比べ
下準備として理解する事項、出力のためのお作法がたくさん増えて厄介です。
理由をかんたんに説明するのは難しいですが、
例えば16という数字は4×4でも計算できますし、32/2でも説明できます。
もっと言えば(3×5)+1とも計算ができます。
この(3×5)+1で計算できるような作りが因子分析で
ぶっちゃけどうとでも計算できてしまうから客観的な評価が重要になってくる
そのためのお作法が細かい、という感じです。
分析っぽくするとこんな図でフムフムするわけですが
これはフムフムレベルがかなり高いやつなので
ざっくり説明なりにここまでいけるよう、今後がんばっていこうと思います。
関連しそうなキーワード:因子負荷量、因子得点、独自性、共通性、最尤法、主因子法、確証的因子分析