ざっくり読み解く 主成分分析【検算もかねて編】
はじめに
今回は過去に紹介した主成分分析の関係性を
実際の計算も踏まえご紹介します。
使用する言語は「R」ですが、需要があればパイソンやVBAでもやっていこうと思います。
データセット
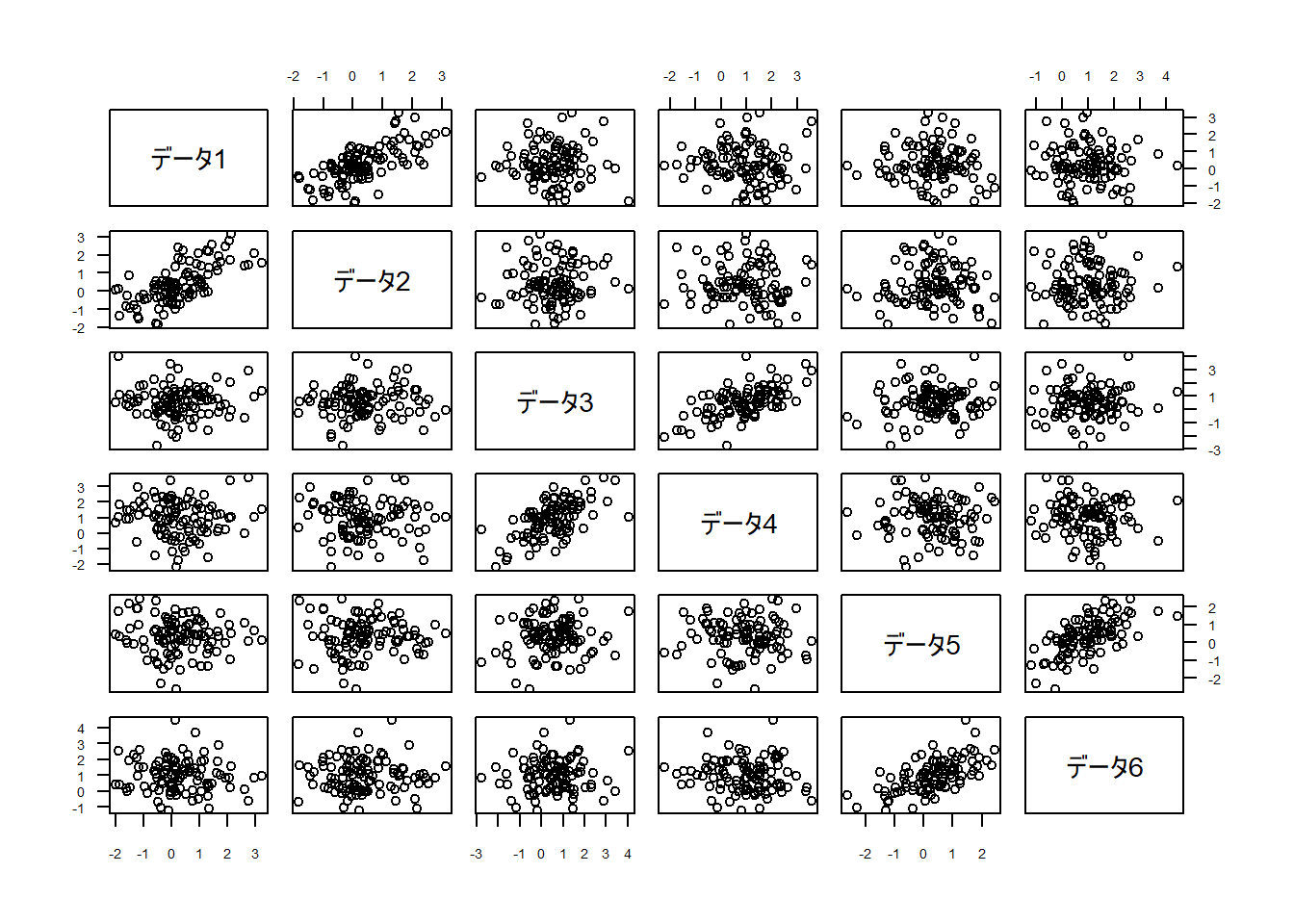
まずは乱数でデータセットの作成。
ライブラリはデフォルトで入っている「MASS」のみ使います。
他にもいろいろ使ってますが、紹介するプログラムには影響ありません。
library(MASS)
set.seed(1)
lam = rbind(
c(0.9,0.9,0,0,0,0),
c(0,0,0.9,0.9,0,0),
c(0,0,0,0,0.9,0.9)
)
rownames(lam) <- paste('fc',1:nrow(lam),sep = '_')
colnames(lam) <- paste('データ' ,1:ncol(lam),sep = '')
lam = t(lam)
sv = lam %*% t(lam)
diag(sv) = 1.2
n = 100
dat = mvrnorm(n,mu = runif(nrow(lam)),Sigma = sv)
colnames(dat) <- rownames(lam)適当な乱数を出力しています。
また再現性のためシードも固定しました。
| データ1 | データ2 | データ3 | データ4 | データ5 | データ6 | |
|---|---|---|---|---|---|---|
| データ1 | 1.157 | 0.783 | 0.007 | -0.064 | -0.097 | -0.070 |
| データ2 | 0.783 | 1.147 | 0.076 | -0.085 | 0.021 | 0.007 |
| データ3 | 0.007 | 0.076 | 1.327 | 0.820 | 0.126 | 0.038 |
| データ4 | -0.064 | -0.085 | 0.820 | 1.347 | -0.044 | -0.088 |
| データ5 | -0.097 | 0.021 | 0.126 | -0.044 | 0.983 | 0.622 |
| データ6 | -0.070 | 0.007 | 0.038 | -0.088 | 0.622 | 1.022 |
par(ps = 8,las = 1)
pairs(dat)主成分分析でおさえたいレシピ
まえに紹介した関係の再掲
※変数のアルファベットを便宜上変えてます。いきあたりばったりですいません。
\[
\begin{array}{l}
Sw = \lambda w\\
\begin{array}{l}
S &=& 対象の行列&:&共分散行列や相関行列など\\
\lambda &=& 固有値&:&加工して累積寄与率などを計算\\
w &=& 固有ベクトル&:&ちょっと加工して主成分負荷量と呼ぶ
\end{array}
\end{array}
\]
さらに後半で紹介した
\[
\begin{array}{l}
S = W \Lambda W^{-1}\\
\begin{array}{l}
S &=& 対象の行列\\
\Lambda &=& 固有値*単位行列したもの\\
W &=& 固有ベクトルを行列に全部くっつけたもの
\end{array}
\end{array}
\]
加えて主成分得点なるものの存在
\[
\begin{array}{l}
Y[,g] = W[,g] \cdot X[i,]\\
\begin{array}{l}
X &=& 元データ\\
W &=& 固有ベクトルを行列に全部くっつけたもの\\
Y &=& 主成分得点行列\\
i &=& 行番号\\
g &=& 列番号\\
\end{array}
\end{array}
\]
また主成分分析で使用するようなデータ形式であれば下記が成り立ちます。
\[
W^{-1} = {}^{t}W
\]
詳細は詳しい方に聞いてください。
固有値計算
固有値の計算は下記の関数でリスト渡しされます。
sv = cov(dat)
buf = eigen(sv)
val = buf$values
vec = buf$vectors| 第1固有値 | 第2固有値 | 第3固有値 | 第4固有値 | 第5固有値 | 第6固有値 | |
|---|---|---|---|---|---|---|
| 固有値 | 2.166 | 1.948 | 1.642 | 0.502 | 0.379 | 0.345 |
固有値ベクトル行列は下記の結果になりました。
| 第1ベクトル | 第2ベクトル | 第3ベクトル | 第4ベクトル | 第5ベクトル | 第6ベクトル | |
|---|---|---|---|---|---|---|
| データ1 | 0.127 | 0.691 | -0.066 | -0.231 | 0.277 | 0.610 |
| データ2 | 0.103 | 0.678 | -0.177 | 0.117 | -0.317 | -0.620 |
| データ3 | -0.688 | 0.161 | -0.092 | 0.650 | 0.250 | 0.083 |
| データ4 | -0.705 | 0.078 | 0.117 | -0.661 | -0.196 | -0.090 |
| データ5 | -0.060 | -0.120 | -0.677 | 0.059 | -0.614 | 0.377 |
| データ6 | -0.008 | -0.129 | -0.695 | -0.264 | 0.587 | -0.294 |
数式の関係性を確認
それではこちらの関係性から
\[
Sw = \lambda w\\
\]
(sv %*% vec) - (diag(val) %*% vec)| col_1 | col_2 | col_3 | col_4 | col_5 | col_6 | |
|---|---|---|---|---|---|---|
| row_1 | 0.000 | -0.150 | 0.035 | 0.384 | -0.495 | -1.110 |
| row_2 | 0.022 | 0.000 | 0.054 | -0.169 | 0.498 | 0.994 |
| row_3 | -0.360 | 0.049 | 0.000 | -0.742 | -0.316 | -0.107 |
| row_4 | -1.173 | 0.113 | 0.134 | 0.000 | 0.024 | 0.014 |
| row_5 | -0.107 | -0.189 | -0.856 | 0.007 | 0.000 | -0.013 |
| row_6 | -0.015 | -0.207 | -0.902 | -0.041 | 0.020 | 0.000 |
いきなり合いませんね。ズコーって感じです。
これは
\[
共分散行列 \cdot 第1ベクトル = 第1固有値 \cdot 第1ベクトル\\
\vdots\\
共分散行列 \cdot 第6ベクトル = 第6固有値 \cdot 第6ベクトル\\
\] と全部同じ結果になるよ(というように辻褄合わせよう)というものなので
正しくは下記の演算
for(g in 1:ncol(dat)){
print(sum(abs(as.numeric(sv %*% vec[,g]) - (val[g] %*% vec[,g]))))
}
## [1] 3.476386e-15
## [1] 2.831069e-15
## [1] 3.053113e-15
## [1] 1.287165e-15
## [1] 8.326673e-16
## [1] 1.19349e-15ということで1つめの計算確認OKです。
つづきまして
\[
S = W \Lambda W^{-1}\\
\]
sv - (vec %*% diag(val) %*% solve(vec))| col_1 | col_2 | col_3 | col_4 | col_5 | col_6 | |
|---|---|---|---|---|---|---|
| row_1 | 0 | 0 | 0 | 0 | 0 | 0 |
| row_2 | 0 | 0 | 0 | 0 | 0 | 0 |
| row_3 | 0 | 0 | 0 | 0 | 0 | 0 |
| row_4 | 0 | 0 | 0 | 0 | 0 | 0 |
| row_5 | 0 | 0 | 0 | 0 | 0 | 0 |
| row_6 | 0 | 0 | 0 | 0 | 0 | 0 |
しっかり0です。
固有値は(固有ベクトルがわかっているのであれば)こんな関係があります。
\[
\Lambda = W^{-1} S W\\
\]
(solve(vec) %*% sv %*% vec)| col_1 | col_2 | col_3 | col_4 | col_5 | col_6 | |
|---|---|---|---|---|---|---|
| row_1 | 2.166 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| row_2 | 0.000 | 1.948 | 0.000 | 0.000 | 0.000 | 0.000 |
| row_3 | 0.000 | 0.000 | 1.642 | 0.000 | 0.000 | 0.000 |
| row_4 | 0.000 | 0.000 | 0.000 | 0.502 | 0.000 | 0.000 |
| row_5 | 0.000 | 0.000 | 0.000 | 0.000 | 0.379 | 0.000 |
| row_6 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.345 |
何れも検算できました。
主成分得点
再掲します。
\[
\begin{array}{l}
Y[,g] = W[,g] \cdot X[i,]\\
\begin{array}{l}
X &=& 元データ\\
W &=& 固有ベクトルを行列に全部くっつけたもの\\
Y &=& 主成分得点行列\\
i &=& 行番号\\
g &=& 列番号\\
\end{array}
\end{array}
\]
そのままプログラム化
Y = dat
for(g in 1:ncol(Y)){
for(i in 1:nrow(Y)){
Y[i,g] = vec[,g] %*% as.numeric(dat[i,])
}
}as.numericは保険のようなものです。
なくても動作する場合もあるし、ないと動作しない場合もある、くらいに覚えておいてください。
総当り的な処理はダセーですという方は
Y = t(t(vec) %*% t(dat))このようにも処理できます。
転置させたり内積、外積をいろいろやるとうまくいきますが
自身でもわからなくなることがあるので必ず検算はしましょう。
さてこの主成分得点はどのような性質があるのか。
平均値
\[
mean(Y) = W^{-1} \bar{X}
\]
as.numeric(solve(vec) %*% apply(dat,MARGIN = 2,mean))
apply(Y,MARGIN = 2,mean)| データ1 | データ2 | データ3 | データ4 | データ5 | データ6 | |
|---|---|---|---|---|---|---|
| 理論値 | -1.002 | 0.451 | -0.934 | -0.528 | 0.273 | -0.279 |
| Yの平均値 | -1.002 | 0.451 | -0.934 | -0.528 | 0.273 | -0.279 |
分散値
\[
var(Y) = W^{-1} S W
\]
diag(solve(vec) %*% cov(dat) %*% vec)
apply(Y,MARGIN = 2,var)| データ1 | データ2 | データ3 | データ4 | データ5 | データ6 | |
|---|---|---|---|---|---|---|
| 理論値 | 2.166 | 1.948 | 1.642 | 0.502 | 0.379 | 0.345 |
| Yの分散値 | 2.166 | 1.948 | 1.642 | 0.502 | 0.379 | 0.345 |
感の良いかたでしたらお気づきと思いますがこの値は\(\lambda\)ですね。
したがって
\[
var(Y) = W^{-1} S W = \lambda
\]
という関係性があります。
というよりは、この関係性を元に \[
\lambda w = Sw
\] が成り立つような\(\lambda\)と\(w\)を計算しようというのが主成分分析(固有値計算)になります。
おそらく他の紹介記事などは順番が逆に書かれていると思います。
個人的にはそれが初学者を振り落とすのではないかなと思い逆にしてご紹介しました。
※かえってわかりにくくなっていたらごめんなさい。
主成分分析の結果との比較
せっかくなのでしかるべきプログラムで計算した主成分分析とも比較します。
res = prcomp(dat)
res$sdev^2
val| データ1 | データ2 | データ3 | データ4 | データ5 | データ6 | |
|---|---|---|---|---|---|---|
| 主成分分析の固有値 (標準偏差) |
2.166 | 1.948 | 1.642 | 0.502 | 0.379 | 0.345 |
| 固有値 | 2.166 | 1.948 | 1.642 | 0.502 | 0.379 | 0.345 |
同じ結果が得られています。
res$rotation| PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | |
|---|---|---|---|---|---|---|
| データ1 | -0.127 | 0.691 | -0.066 | 0.231 | 0.277 | -0.610 |
| データ2 | -0.103 | 0.678 | -0.177 | -0.117 | -0.317 | 0.620 |
| データ3 | 0.688 | 0.161 | -0.092 | -0.650 | 0.250 | -0.083 |
| データ4 | 0.705 | 0.078 | 0.117 | 0.661 | -0.196 | 0.090 |
| データ5 | 0.060 | -0.120 | -0.677 | -0.059 | -0.614 | -0.377 |
| データ6 | 0.008 | -0.129 | -0.695 | 0.264 | 0.587 | 0.294 |
vec| 第1ベクトル | 第2ベクトル | 第3ベクトル | 第4ベクトル | 第5ベクトル | 第6ベクトル | |
|---|---|---|---|---|---|---|
| データ1 | 0.127 | 0.691 | -0.066 | -0.231 | 0.277 | 0.610 |
| データ2 | 0.103 | 0.678 | -0.177 | 0.117 | -0.317 | -0.620 |
| データ3 | -0.688 | 0.161 | -0.092 | 0.650 | 0.250 | 0.083 |
| データ4 | -0.705 | 0.078 | 0.117 | -0.661 | -0.196 | -0.090 |
| データ5 | -0.060 | -0.120 | -0.677 | 0.059 | -0.614 | 0.377 |
| データ6 | -0.008 | -0.129 | -0.695 | -0.264 | 0.587 | -0.294 |
一見符号が合いませんが、これは大人の都合です。
主成分得点はどうでしょうか。
相関係数1ということで一見すると完全に一致しています。
apply(res$x,MARGIN = 2,mean) apply(Y,MARGIN = 2,mean)
| データ1 | データ2 | データ3 | データ4 | データ5 | データ6 | |
|---|---|---|---|---|---|---|
| 主成分得点の平均値 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Yの平均値 | -1.002 | 0.451 | -0.934 | -0.528 | 0.273 | -0.279 |
ただし平均値は合いません。これは主成分分析の都合上、平均値をゼロに馴らしたほうが良いという判断からでしょう。
一連の計算処理で一通りの計算が確認できたかと思います。
自作の固有値、固有ベクトル計算などを開発した折には活用してみてください。