指数分布について｜Excel（エクセル）で学ぶデータ分析ブログ

指数分布とは？

Wikipediaより(一部編集)
指数分布(exponential distribution)とは、確率論および統計学における連続確率分布の一種である。ある離散的な事象に対して、ポアソン分布が単位時間当たりの生起確率を示し、指数分布は生起期間の確率を示す。

指数分布の仕組み

指数分布はガンマ分布の特殊ケース(α=1のとき)です。

\[
f(x; \alpha , \beta) = \frac{\beta ^ \alpha}{\Gamma(\alpha)} x^{\alpha – 1} \exp(- \beta x) ~~~ (0 < x)
\]

---

\[
\alpha = 1 , \beta = \lambda　のとき \\
f(x; 1 , \lambda) = \frac{\lambda ^ 1}{\Gamma(1)} x^{1 – 1} \exp(- \lambda x)\\
= \lambda \exp(- \lambda x)
\]

ということで、下記のように整理されます。

\[
f(x;\lambda) =
\left\{
\begin{array}{ll}
\lambda \exp(-\lambda x) & (0 \leq x) \\
0 & (x < 0)
\end{array}
\right.
\]

また、ポアソン分布と指数分布は同じ事象の捉える角度を変えることでリンクさせられるので同様に紹介されることが多いです。 \[
p(X=x) = \exp(-\lambda) \frac{\lambda^x}{x!}
\]

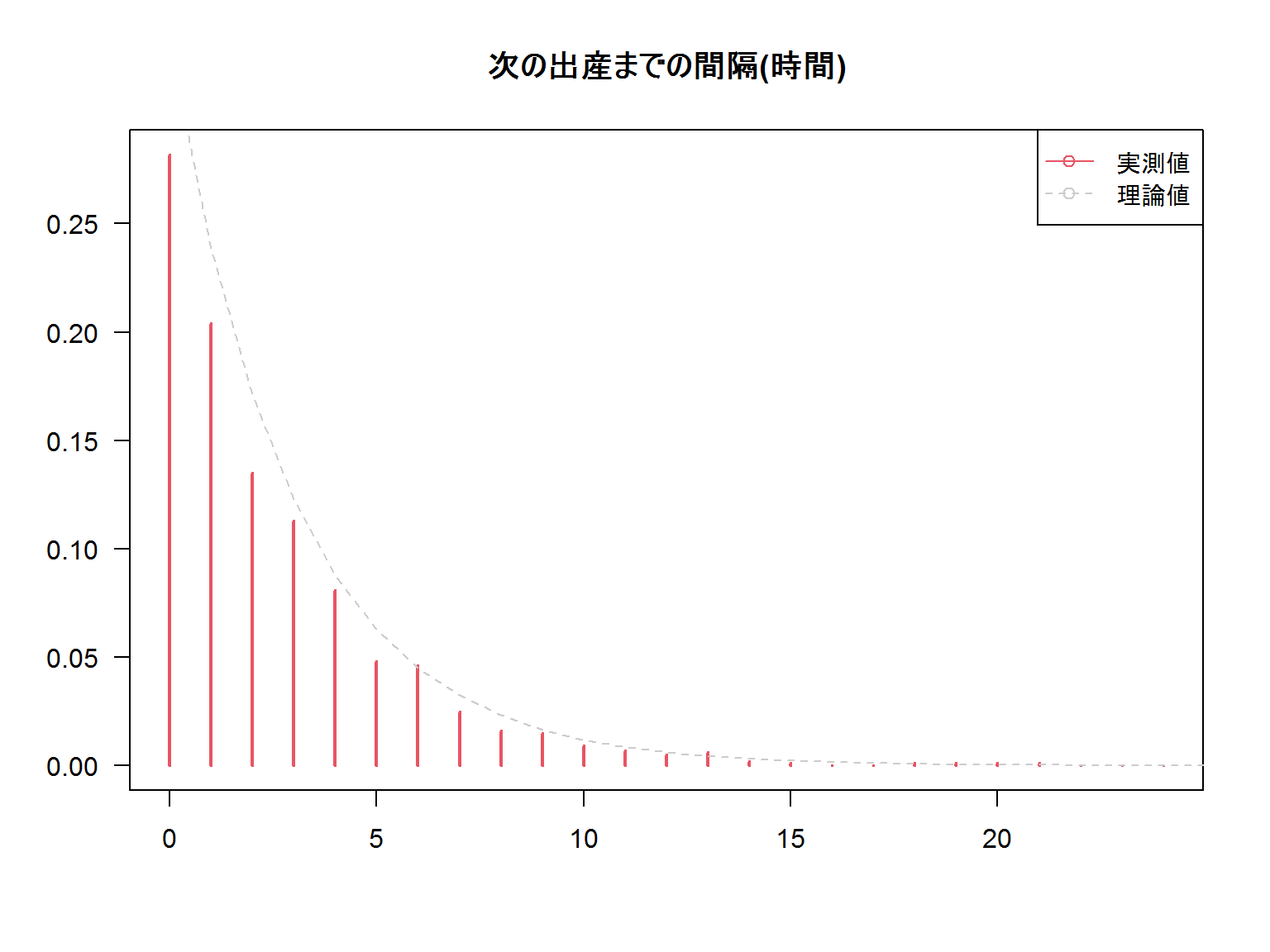
よく「ラットの生存時間」とか「機械が故障するまでの時間」というものを題材に説明することが多いですが
今回は縁起がいい感じで産婦人科の出産率を題材に考えようと思います。

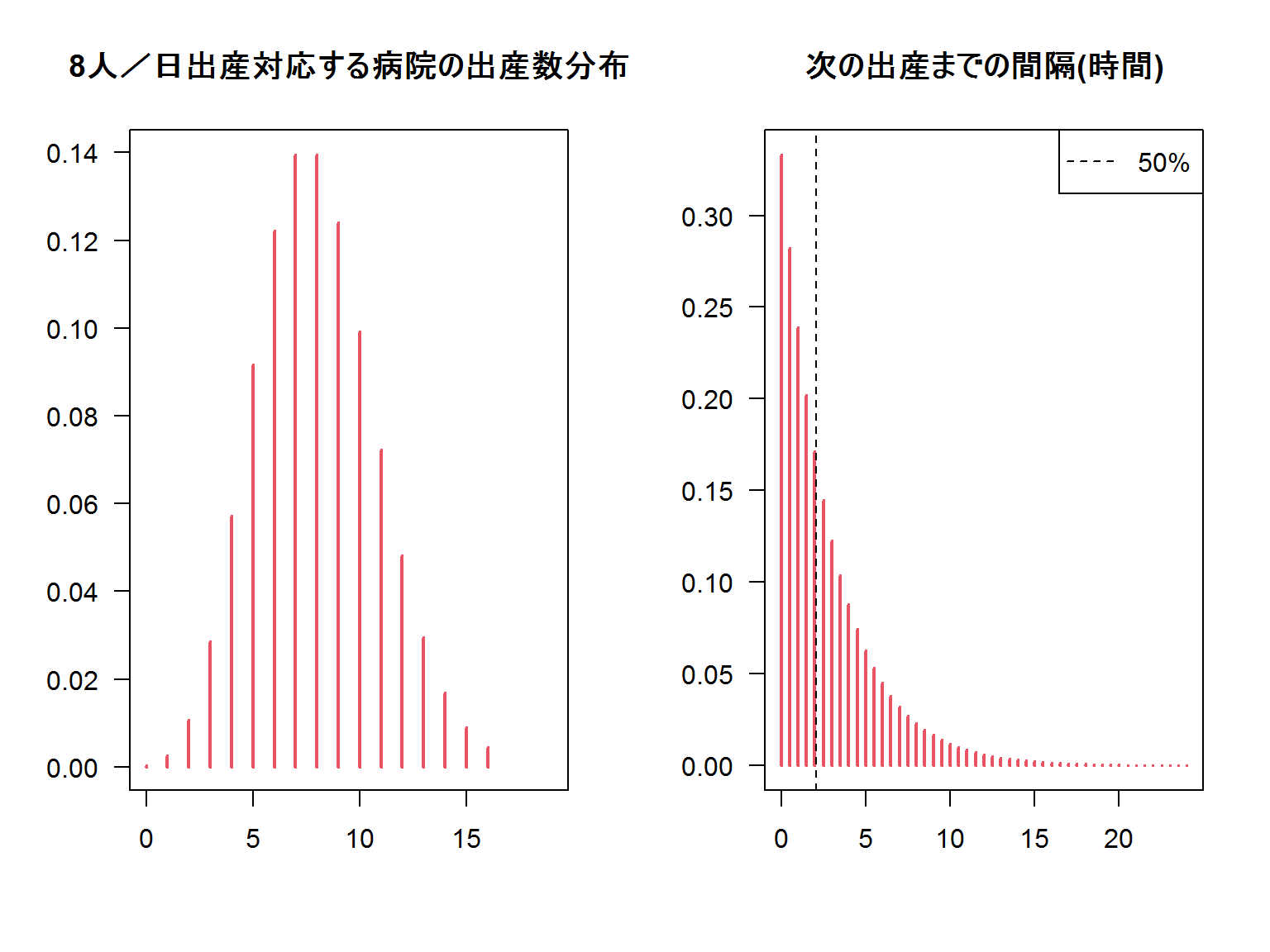
ポアソン分布のパラメータは\(\lambda = 8\)で
指数分布のパラメータは\(\lambda = 8*(1/24)\)になります。
およそ50%の確率で2時間以内に次の出産が入ることが予測できました。

乱数のシミュレーション

次は、同様の事象を乱数でシュミレーションします。
上記の指数分布に従う確率で1日あたりの出産対応数を集計しました。

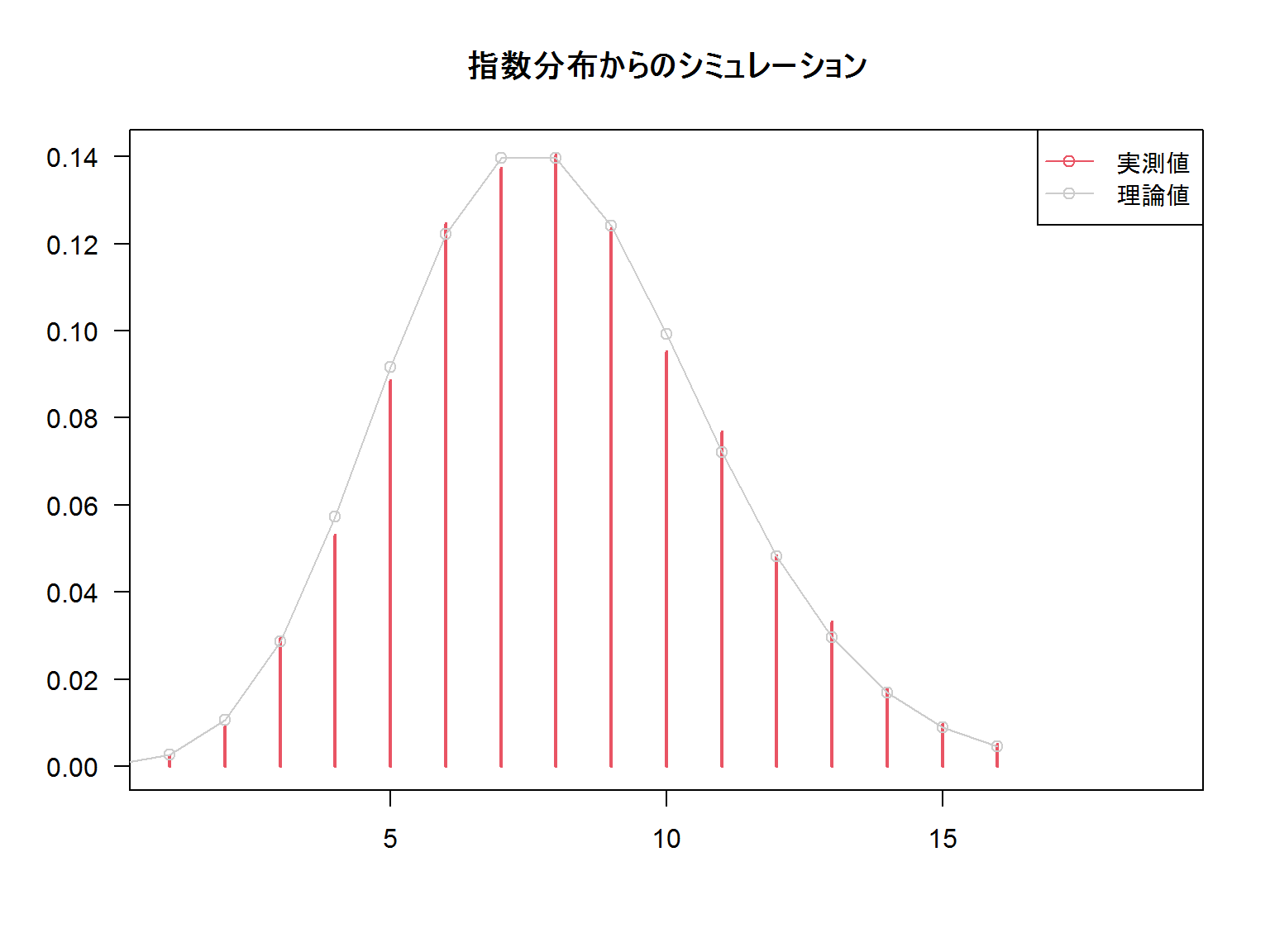
うまく当てはまっていることがわかります。

今度は、一様乱数を使用して
指数分布にしたがう事象をシミュレーションしました。
連続性を出すために1/100万単位の乱数を10,000回出力するという荒業で生起確率を計算しました。
筆者(というよりPCが悲鳴を上げております)

エクセルでは下記のようにあらわします。

=B$1*EXP(-B$1*$A2)

=EXPONDIST($A2,B$1,0)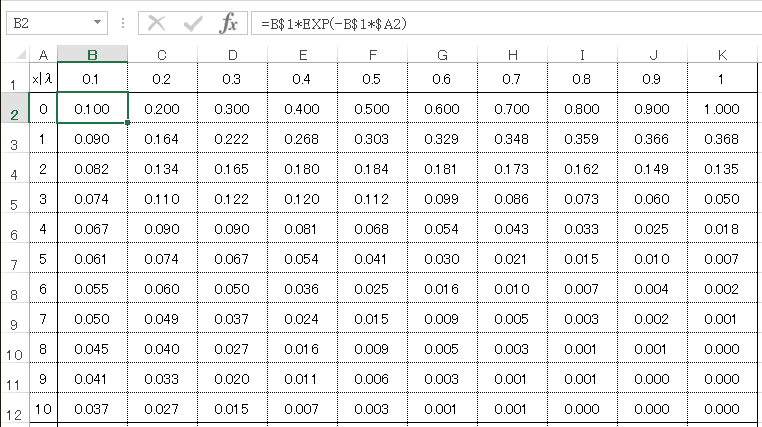

指数分布と幾何分布

指数分布と幾何分布を見比べると、どことなく性質(構成)が似ているように感じます。 \[
f(x;\lambda) =
\left\{
\begin{array}{ll}
\lambda \exp(-\lambda x) & (x \geq 0) \\
0 & (x < 0)
\end{array}
\right.
\]

\[
p(X=x) = p (1-p)^{x-1}
\]

それぞれに同じパラメータを与えてみましょう。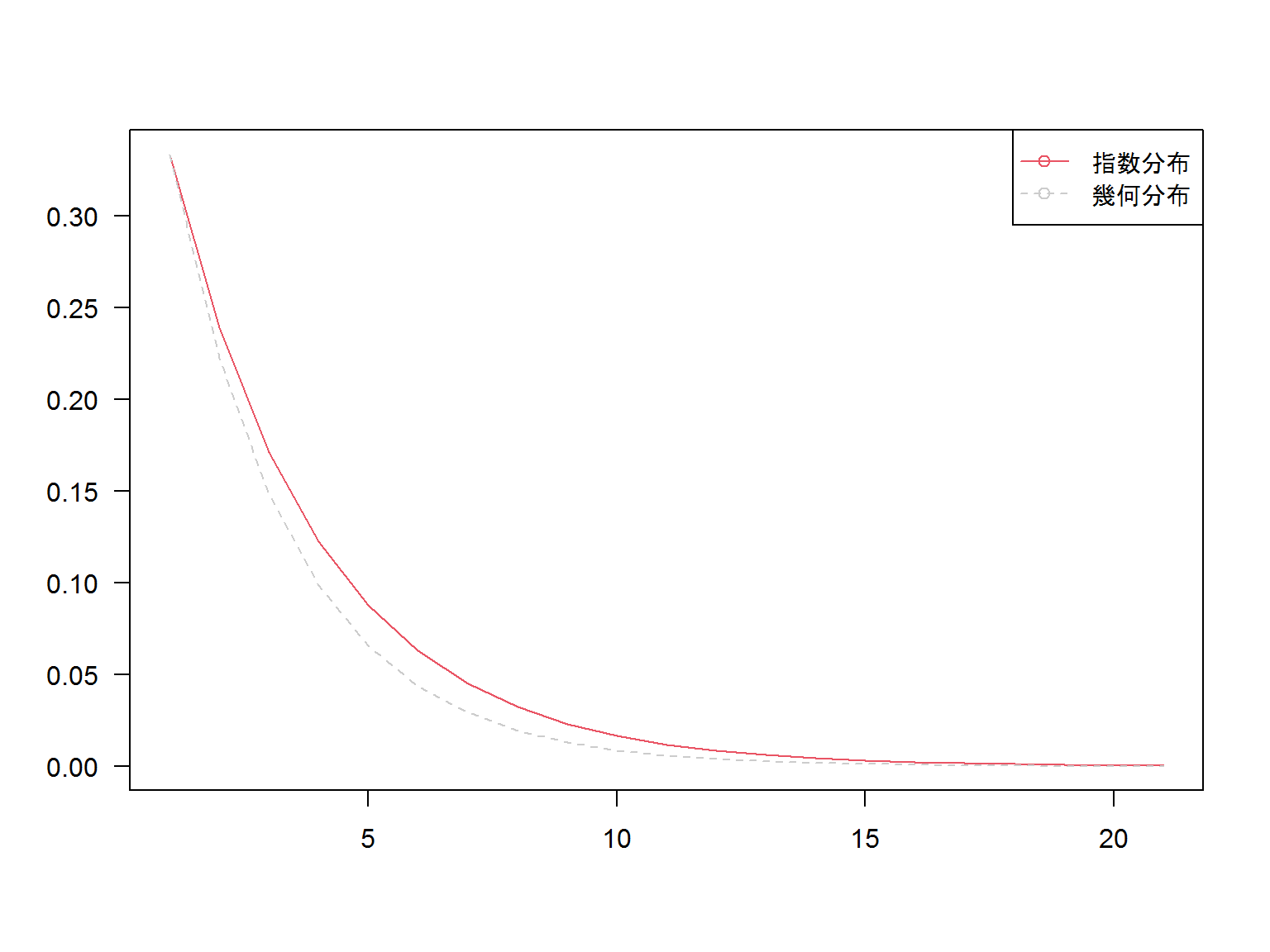 

感覚的な理解としては幾何分布に
・連続性を出す
・par(0≦%≦1)の範囲を拡張させる
ようなイメージでしょうか。
ということは、ガンマ分布と負の二項分布も似たようなものなのでしょうか。

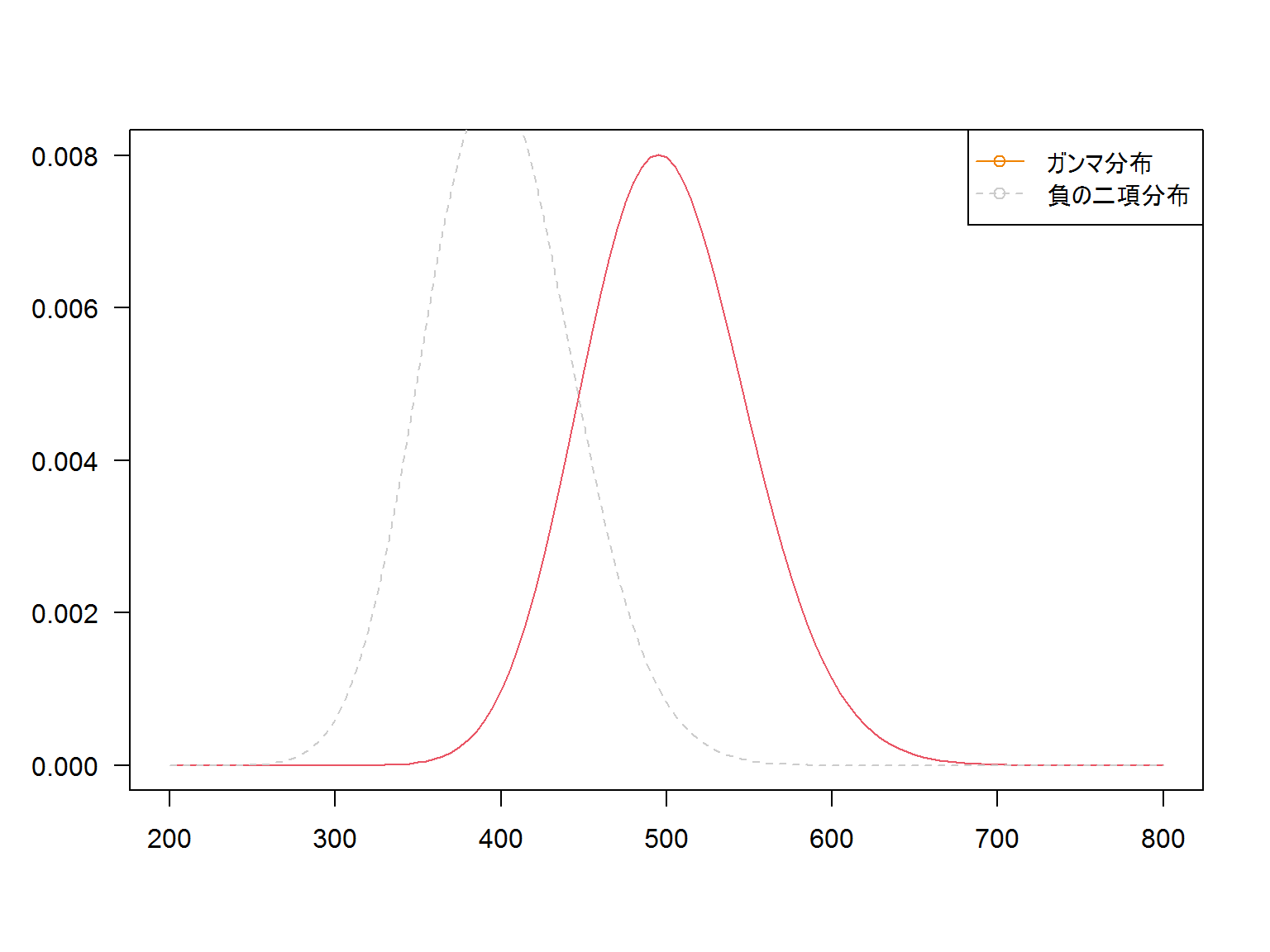
…なんとなく、似ているように感じます。