超幾何分布について|Excel(エクセル)で学ぶデータ分析ブログ
超幾何分布とは?
Wikipedia より(一部編集)
超幾何分布(Hypergeometric distribution)は、成功状態をもつ母集団から非復元抽出したときに成功状態がいくつあるかという確率を与える離散確率分布の一種である。
二項分布や幾何分布を理解していれば、超というほどの難しさではありませんのでご安心ください。
超幾何分布の仕組み
全個数N個、アタリの玉とハズレの玉を箱のなかに入れたとします。
この中から非復元抽出(取ったものを戻さない)でn個順番に取り出す試行を考えます。
全個数N個からn個取り出す組み合わせは\({}_NC_n\)通り考えられるので、まずこれを念頭に置いてください。
次に、N個のうちアタリ玉の数をM個とすると、ハズレ玉は\(N-M\)個になります。 ここで、n個玉を抜き出したときにアタリ玉をx個取った組み合わせを考えます。
アタリ玉を取る組み合わせは\({}_{M}C_{x}\)と同時にハズレ玉を取る組み合わせ\({}_{N-M}C_{n-x}\)を掛けた
\({}_{M}C_{x} \times {}_{N-M}C_{n-x}\)通り考えられます。
\[
\binom{アタリ玉}{アタリ玉を引いた個数} \times \binom{全個数-アタリ玉}{引いた個数-アタリ玉を引いた個数}
\]
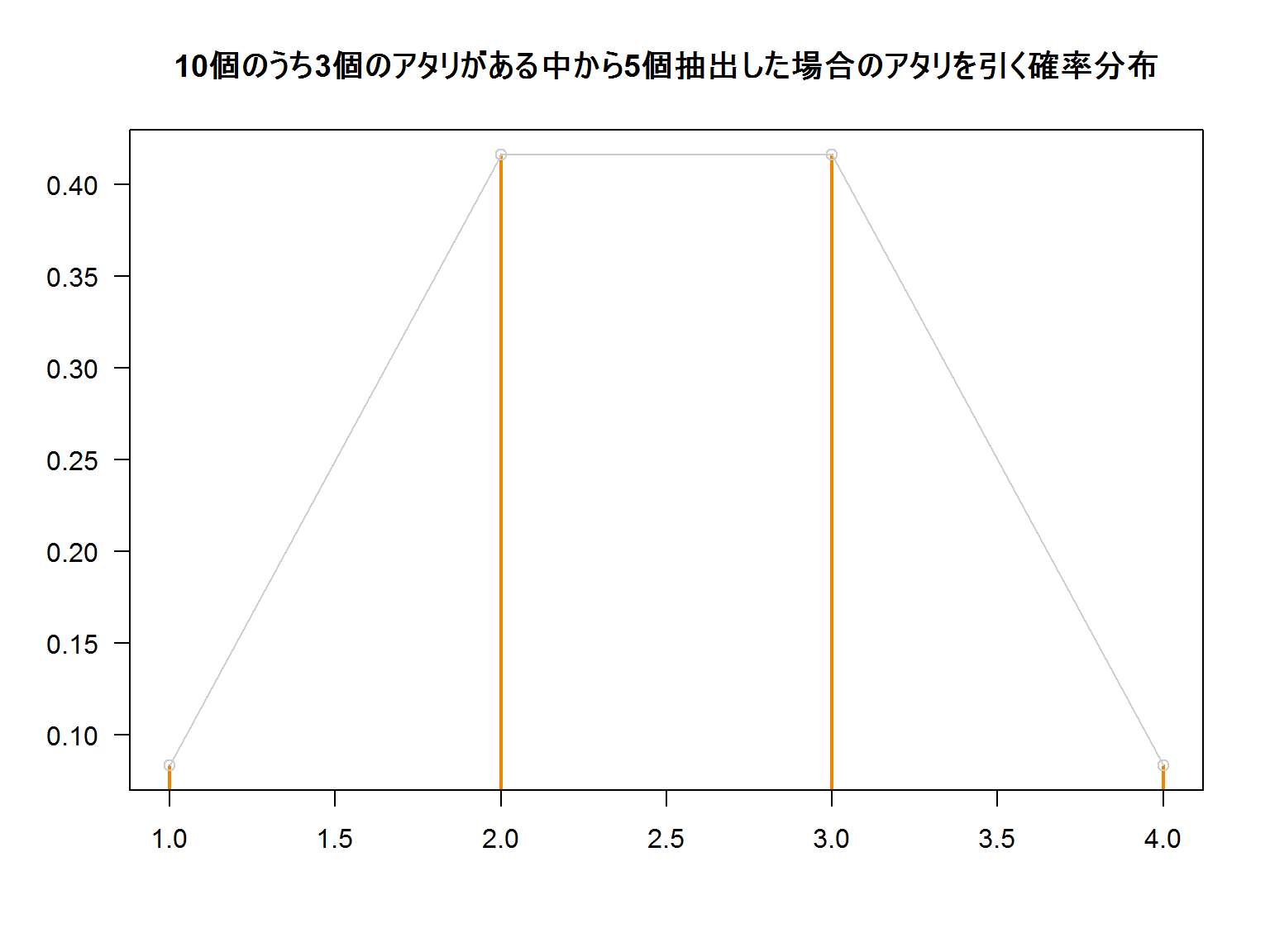
わかりやすく、N=10個としてアタリ玉を3個、順番に5回取った場合の組み合わせを考えます。
アタリ=3 \[
{}_{3}C_{3} \times {}_{10-3}C_{5-0} = 21
\]
アタリ=2 \[
{}_{3}C_{2} \times {}_{10-3}C_{5-1} = 105
\]
アタリ=1 \[
{}_{3}C_{1} \times {}_{10-3}C_{5-2} = 105
\]
アタリ=0 \[
{}_{3}C_{0} \times {}_{10-3}C_{5-3} = 21
\]
感の良い方ならお分かりと思いますが上記の組み合わせを合計した値は\({}_NC_n\)と一致しますので \[
\sum_{x=0}^{n} {}_{M}C_{x} \times {}_{N-M}C_{n-x} = {}_NC_n
\] となります。
まとめると \[
P(X=x) = \frac{ {}_{M}C_{x} \times {}_{N-M}C_{n-x} }{ {}_NC_n }
\] という超幾何分布が作れました。
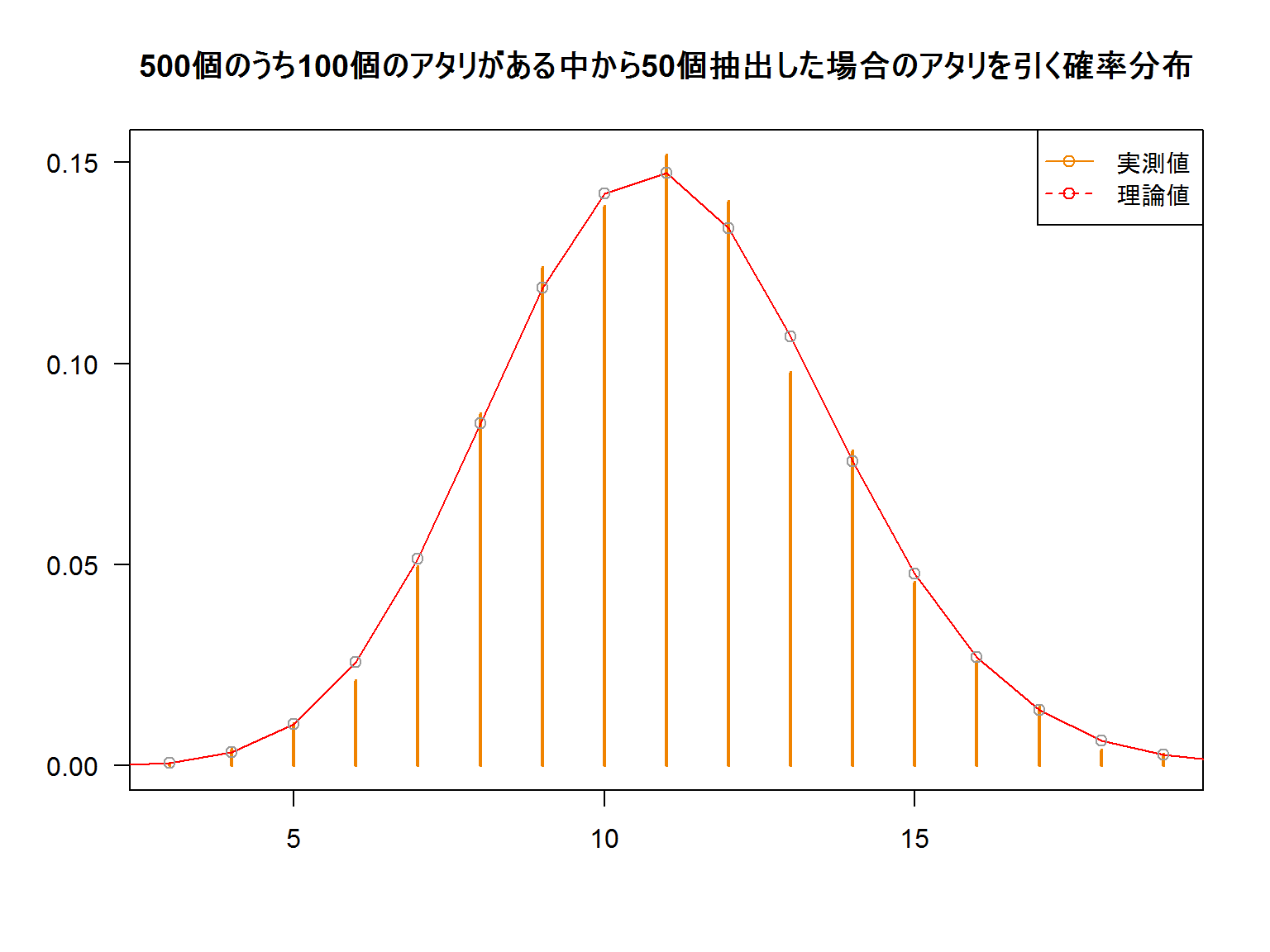
乱数のシミュレーション
500個中100個アタリの入った箱から50回取ってみてアタリの分布がどうなるのか5,000回ほど試行してみました。
エクセルでは下記のようにあらわします。
全個数10個から:5個抜き出した場合
=(COMBIN(B$1,$A2)*COMBIN(20-B$1,5-$A2))/COMBIN(20,5)=HYPGEOMDIST($A2,5,B$1,20)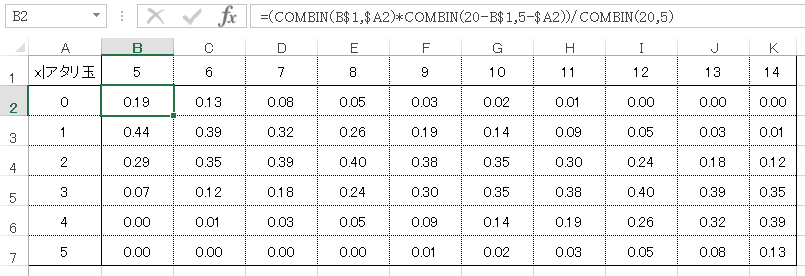
超幾何分布を極端に考えてみる。
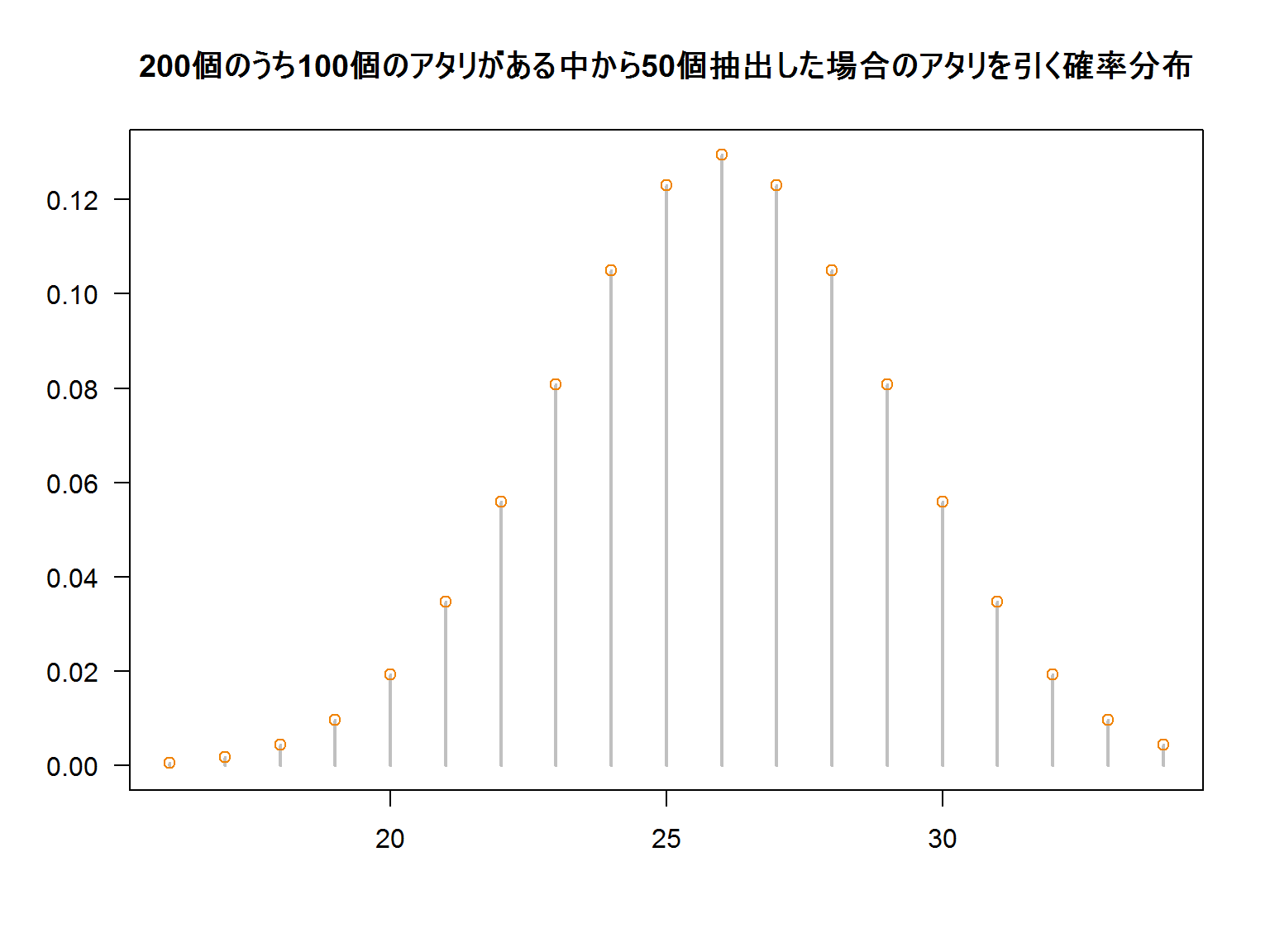
上記のグラフを見ていると、なんとなく二項分布に近似しそうな気がします。
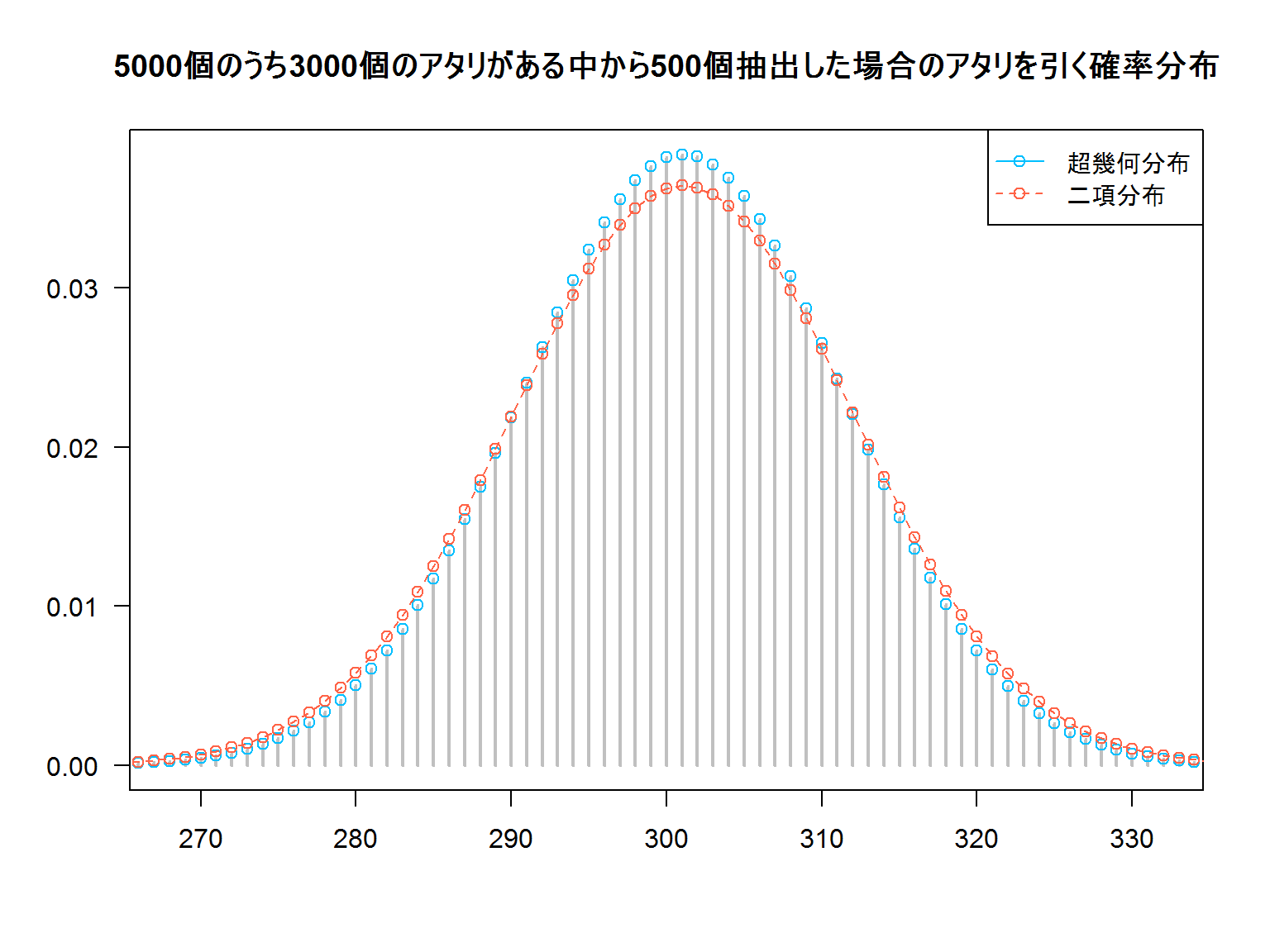
N個中のアタリ数を一定(\(M/N \to p\))にし、Nを無限(\(N \to \infty\))に近づけていくと、超幾何分布は二項分布に近似します。
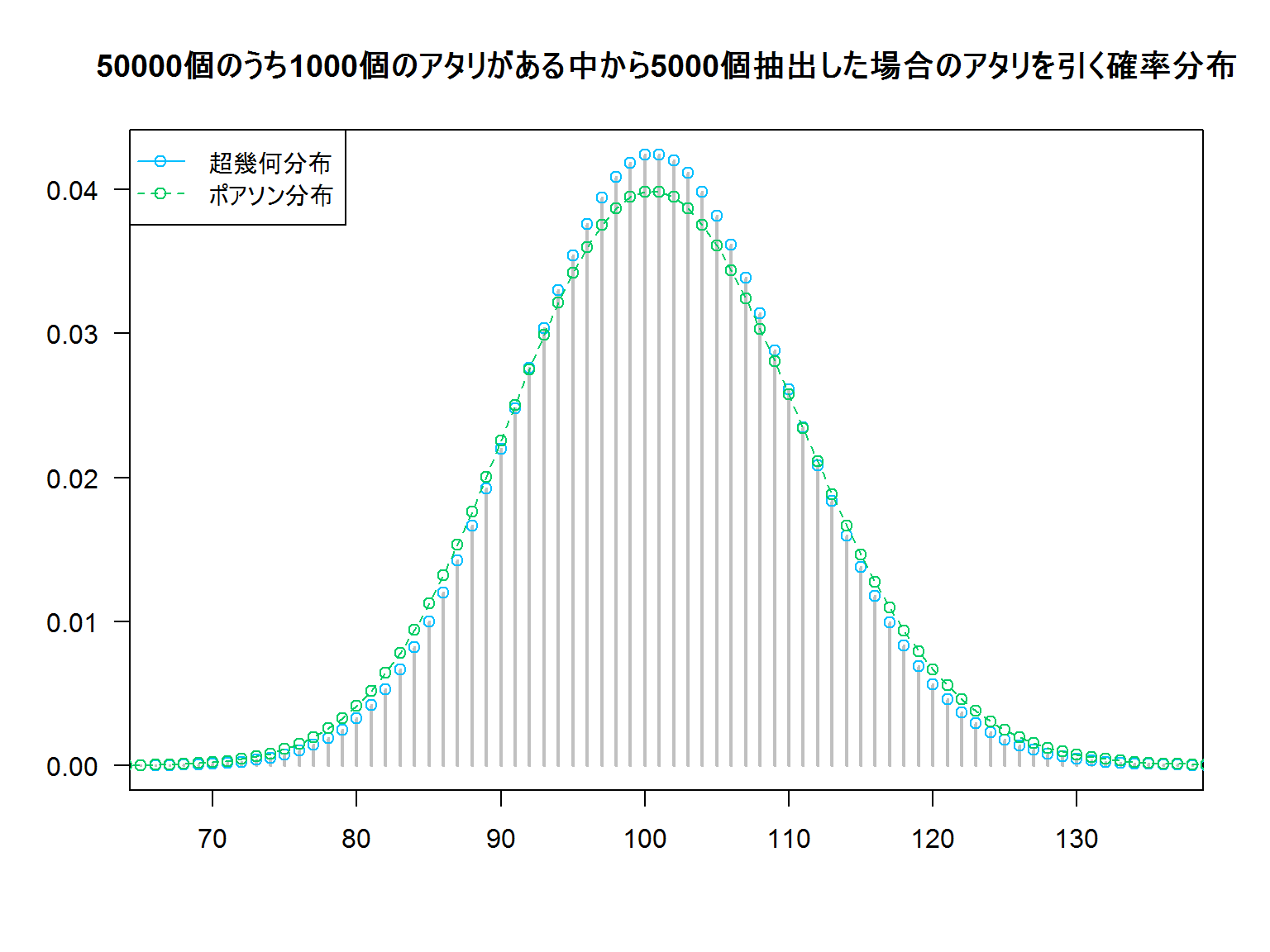
また、N個中のアタリ数の比率を小さく、抽出数(n)をある程度の大きくしていくと、超幾何分布はポアソン分布に近似します。